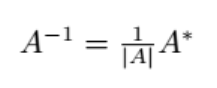一些废话
涉及线代 矩阵 概率论 多元随机变量 数字特征 期望 相关系数
推荐书目
- 应用多元统计分析 –王学民
- 数据统计分析
- 统计学习方法 李航
1 矩阵代数(基础)
1.1 定义
1.2 矩阵的运算
1.3 行列式
1.4 矩阵的逆
1.5 矩阵的秩
1.6 特征值、特征向量、矩阵的迹
1.7 正定矩阵和非负定矩阵
1.8 特征值的极值问题
2 随机向量
多元分布
数字特征
欧氏距离、马氏距离
随机向量的变换
特征函数
3 多元正态分布
3.1 定义
3.2 性质
3.3 极大似然估计以及估计量的性质
3.4 复相关系数和偏相关系数
3.5 $\overline{x}$和 (n-1)S 的抽样分布
4 多元正态总体的统计推断
4.1 一元情形
4.2 单个总体均值的推断
4.3 两个总体均值的比较推断
4.4 轮廓分析
4.5 多个总体均值的比较检验(多元方差分析)
4.6 协方差矩阵相等性的检验
4.7 总体相关系数的推断
5 判别分析
引言
距离判别
贝叶斯判别
费希尔判别
逐步判别
6 聚类分析
引言
距离和相似系数
系统聚类法
动态聚类法
7 主成分分析
引言
总体的主成分
样本的主成分
若干补充及主成分应用中需注意的问题
8 因子分析
引言
正交因子模型
参数估计
因子旋转
因子得分
9 对应分析
引言
行轮廓和列轮廓
独立性检验和总惯量
行、列轮廓的坐标
对应分析图
10 典型相关分析
引言
总体典型相关
样本典型相关
典型相关系数的显著性检验
——————————————————————————————————————————————
第一章 主要对多元统计分析 是什么有个大致概念
多元是多维度
多元统计分析是一种统计方法,用于分析多个变量之间的关系。它通过同时考虑多个变量,帮助我们理解数据的结构和模式。以下是一些常见的多元统计分析方法:
- 主成分分析(PCA):用于降维,通过将原始变量转换为一组不相关的主成分来减少数据的维度。
- 因子分析:用于识别潜在的变量(因子),这些变量解释了观察到的变量之间的相关性。
- 聚类分析:用于将数据分组,使得同一组内的数据点彼此相似,而不同组的数据点差异较大。
- 判别分析:用于分类,确定观测值属于哪个预定义的类别。
- 多元回归分析:用于预测一个因变量与多个自变量之间的关系。
这些方法广泛应用于各个领域,如市场研究、金融分析、生物医学研究等。通过多元统计分析,可以更全面地理解数据,做出更准确的预测和决策。
第二章 随机变量回顾
数值特征描述:一元情况下 总体和样本
总体

总体可以筛选出样本,以下是样本均值 样本方差 样本标准差的计算方法
样本

样本方差的公式如下:
$[ s^2 = \frac{1}{n-1} \sum_{i=1}^{n} (x_i – \bar{x})^2 ]$
计算样本方差时,分母用 ( n-1 ) 是为了纠正由于样本均值与总体均值的差异导致的计算误差。这样做可以使得样本方差更接近真实的总体方差,从而得到一个无偏估计。这个调整称为贝塞尔校正(Bessel’s correction)。
更为详细的解释:

换言之:样本方差实际上是对总体方差的预测值。通过使用 ( n-1 ) 作为分母进行贝塞尔校正,我们得到的样本方差是总体方差的无偏估计。因此,样本方差并非仅仅描述样本本身的离散程度,而是用于估计总体的离散程度。
数值特征描述:二元随机变量(X,Y) 总体和样本
总体协方差Covariance 刻画变量线性关系
协方差为正代表两变量正向线性相关,为负则代表负向线性相关,其绝对值越大,代表线性相关性越强。
用于衡量两个变量的总体误差,方差是协方差的一种特殊情况,两个变量是相同的情况

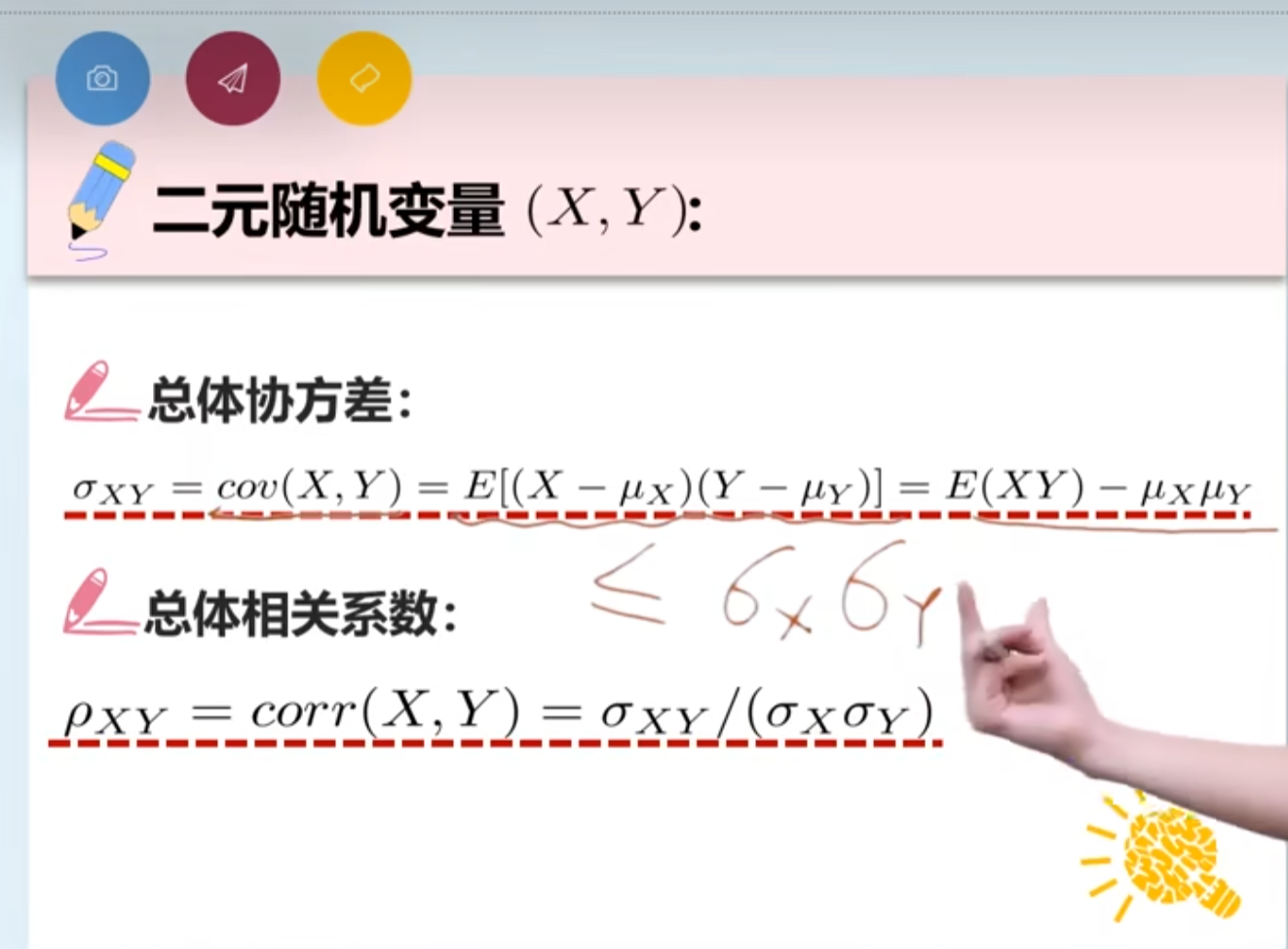
总体相关系数
总体相关系数(线性相关系数,或者叫皮尔逊相关系数)
$covariance(X,Y)≤σ_xσ_y$ 把右边除到左边
就得到了$ρ_{X,Y}$ 其取值范围为【-1,1】,绝对值越大相关性越强,若为0则代表没有线性相关性,但不一定不相关

样本:协方差、相关系数

注:
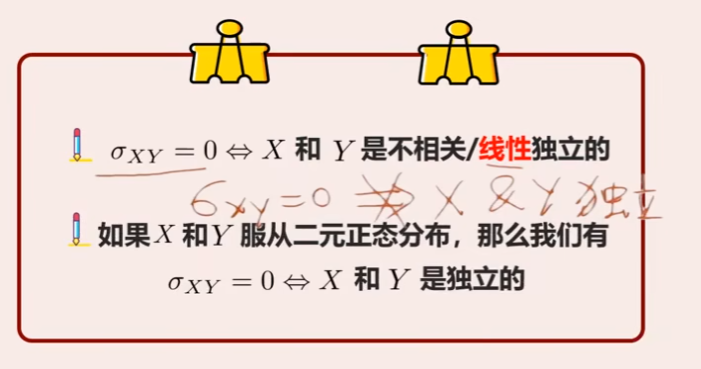
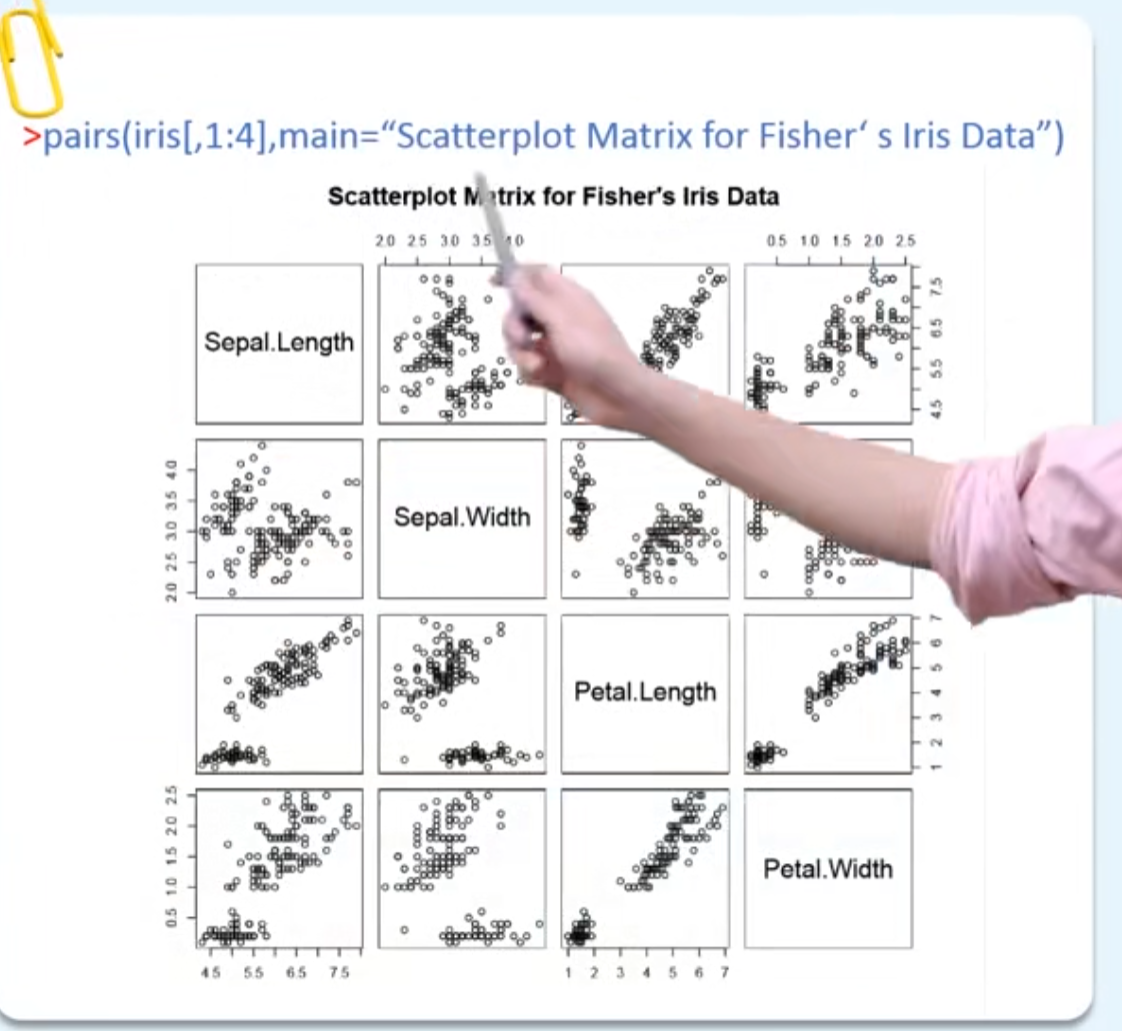
可视化 (有意思
一维散点图例子
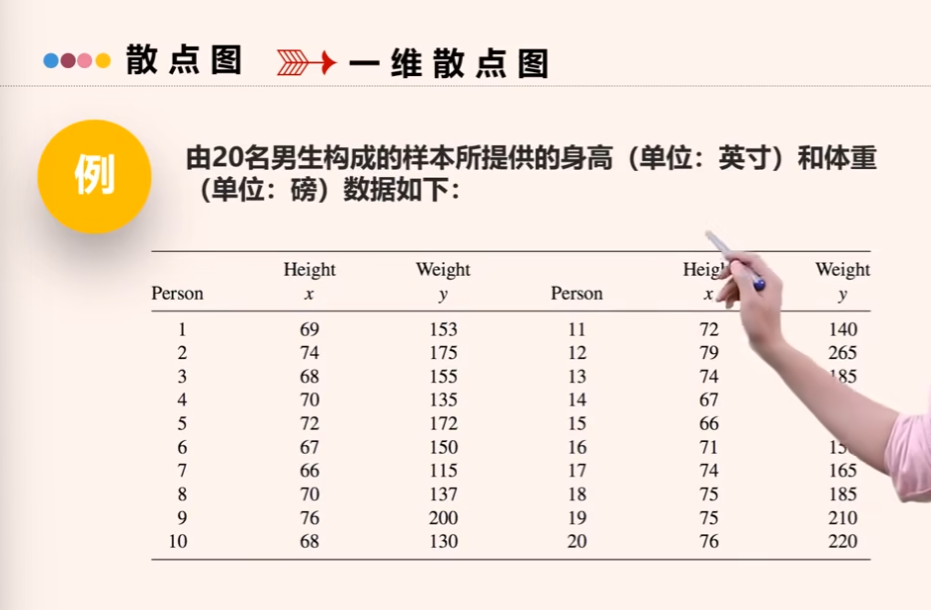
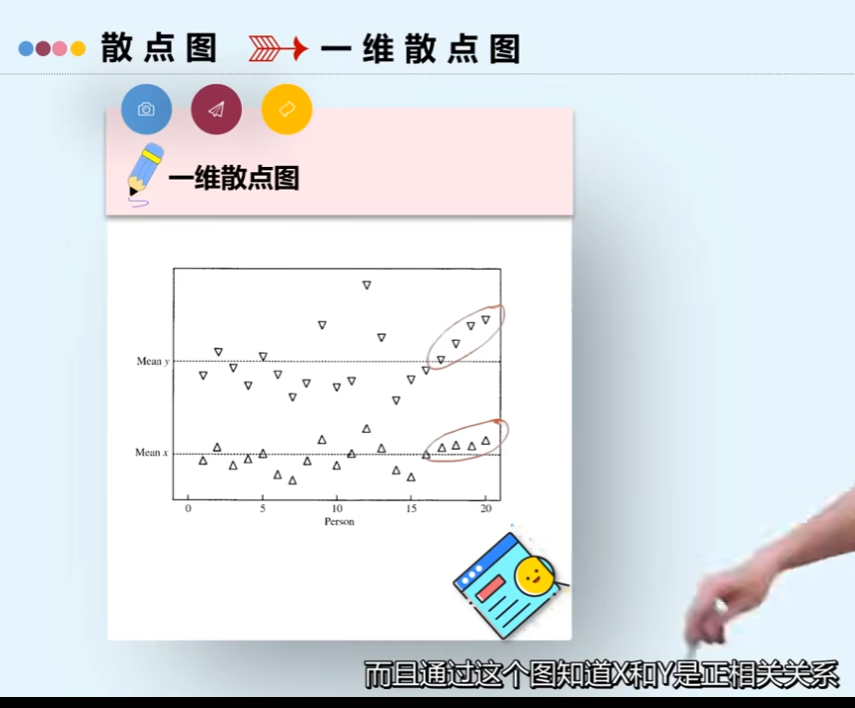
为了更清晰看出二者相关关系,可以画二维散点图
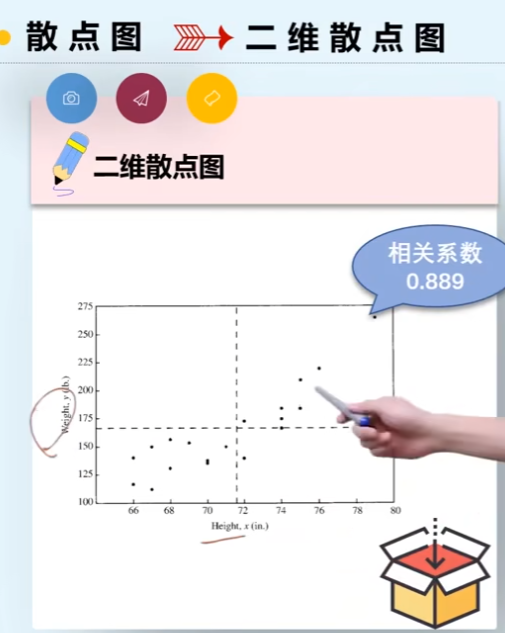
随机向量
多元数据的数值特征以及可视化

协方差矩阵

样本协方差矩阵,类似总体和样本的方差,除以n-1

协方差矩阵是对称阵,其中一个例子:因为$σ_{jk}=σ_{kj}$



可视化