核心:线性方程组
工具:
- 行列式
- 矩阵
- 向量
行列式的本质是一个数或者含有字母的式子
1、定义
1.1、逆序

1.2、逆序数
排列中逆序的总数
3 1 2 可以构成的逆序有31 32所以t(312)逆序数=2
2341 可以构成的逆序有21 31 41所以t(2341)逆序数=3
t(35142)=31 32 51 54 52 42 =6
1.3、行列式
nxn=n阶行列式
特解三阶行列式

遇到的问题:计算行列式如何判断其中某项的正负
Q:保证行序逐渐增大,通过列序来判断逆序数;由列标排列的【逆序数】决定——奇负偶正
重:这个和下面代数余子式容易搞混
1.4、余子式/代数余子式
取aij的i行j列元素全部划去,留下的式子为aij的余子式
余子式前面加个系数为aij的代数余子式
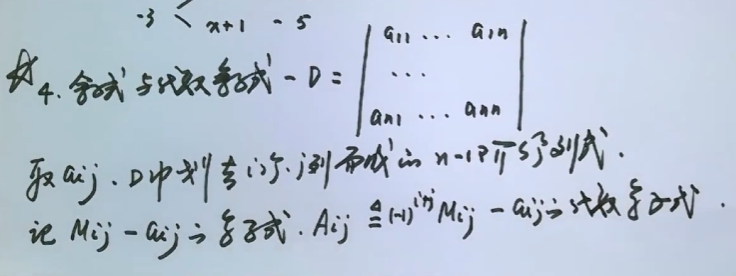
2、特殊
2.1、主对角线行列式,上三角行列式,下三角行列式
求解:主对角线相乘
2.2、范德蒙行列式
第一行是1,第二行是a1到an,第三行是a1^2到an^2,第n行是a1^(n-1)到an^(n-1)

求解:通过特例推出通解,从V2开始,(a2-a1) ;
V3=(a3-a1)(a3-a2)(a2-a1);
V4=(a4-a1)(a4-a2)(a4-a3)(a3-a1)(a3-a2)(a2-a1)
重点:Vn!=0 充要条件 a1、a2、…. 、an互不相等
2.3、正方块行列式
其中A和B是正方块
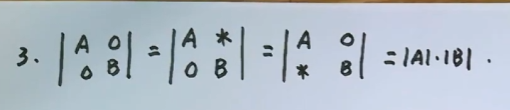
3、行列式的计算性质
- 行列式的转置等于本身
- 对调两行/列 行列式变符号
- 一行/列有公因子可以提出去
- 行列式可拆
- 一行/列 的k倍加到另一行/列 行列式不变!!
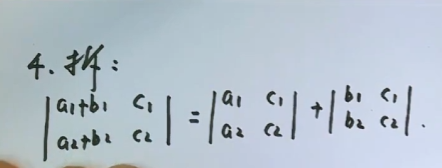
3.1例1 直接计算
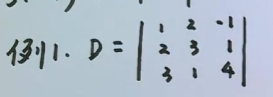
方法是通过等价变换行列式为上三角行列式,直接算出

3.2、例2 识别全部加到一行 提取公因式
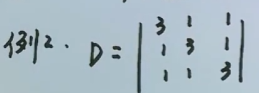
全部加到第一行,提出公因子再化三角

3.3、例3 行列式拆分+基础性质
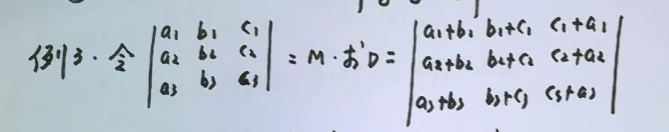

4、降阶性质
行列式等于某一行元素乘以其对应代数余子式

什么时候用?什么时候这个性质在计算行列式时有优势?
当某一行/列0元素特别多,可以按该行/列展开,既降阶,又能尽可能最小化数量
两个性质,一行乘以对应的代数余子式相加是原来的,其他行乘以非对应其他的代数余子式是为0

A* A的伴随矩阵
Mij 余子式 Aij代数余子式

行列式见到代数余子式Aij或者A*伴随矩阵
用两个工具
$|A^*|=|A|^{n-1}$
$|A|=a_{i1}A_{i1}+…+a_{in}A_{in}$



