行列式是一个数或一个式子，矩阵是一个表格

1、定义

1.1、方阵、零矩阵

1.2、同型矩阵

2、三则运算

2.1、加减法

矩阵相加减，是每个位置对应相加减，跟行列式区别开，行列式是可以拆分某一行某一列

2.2、乘法

矩阵乘法，内标同可乘，外标定型

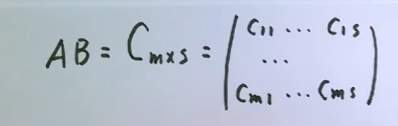
cij=ai1+b1j + ai2b2j + ai3b3j+…+ain bnj

3、注意

3.1 ”非0矩阵相乘可得0矩阵“

A矩阵和B矩阵都不为0矩阵，但是AB 不一定不是0矩阵

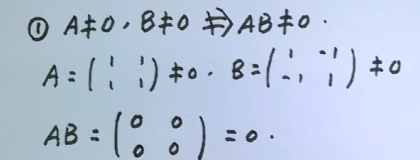
3.2 “非零矩阵k次方可为0”

3.3″AB与BA不一定等”

好理解，ab和ba甚至可以不同型

3.4 fx =anx^n+…+a1x+a0

给定Anxn A的矩阵多项式

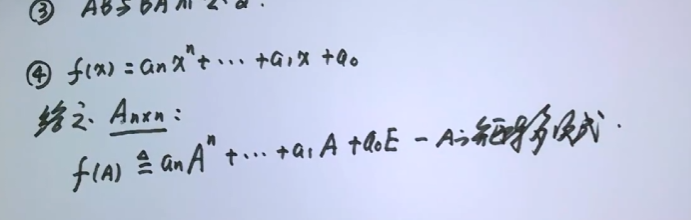
矩阵多项式可以像多项式一样因式分解的

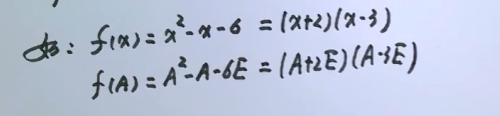
3.5 线性方程组一般形式

等于0的为齐次线性方程组

不等于0的为非齐次线性方程组

矩阵化，模块化

AX=0代表齐次线性方程组

AX=B代表非齐次线性方程组

矩阵是研究方程组的重要工具

3.6 A左乘B，左边乘以右边列化

3.6跟3.7一句话 矩阵乘法：左矩阵确定行 右矩阵确定列

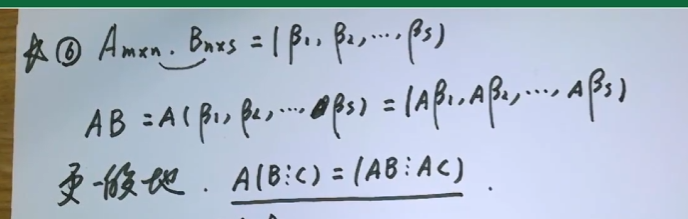
B有很多列，C有很多列 AB AC直接乘

3.7 左列化，右具体化

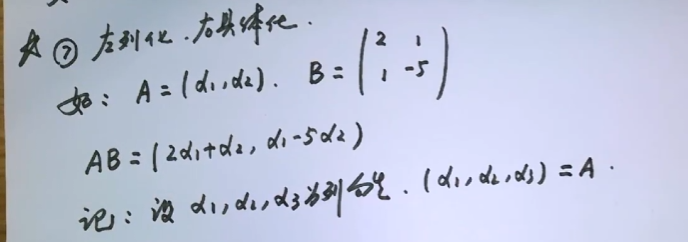
把B拆分成两个矩阵

4 伴随矩阵

得注意伴随矩阵的样子，第一列行标为1 第二列行标为2 ，行标与列表是与原来矩阵反着来的，这是为了满足AA*=|A|E 为了满足而凑出来的？

余子式本质是一个行列式

Mij是原来矩阵去掉第i行第j列所有元素后形成矩阵的行列式

Aij是代数余子式

注意！ AA* 乘 运用降阶性质 一行元素乘以其代数余子式为本身/乘以其余行为0

AA*=A*A=|A|E 很严谨，为A的行列式 x 单位阵 单位阵的大小由AA*确定

要想搞懂AA*乘起来到底是什么，要先有下面的理论基础 按行按列展开性质

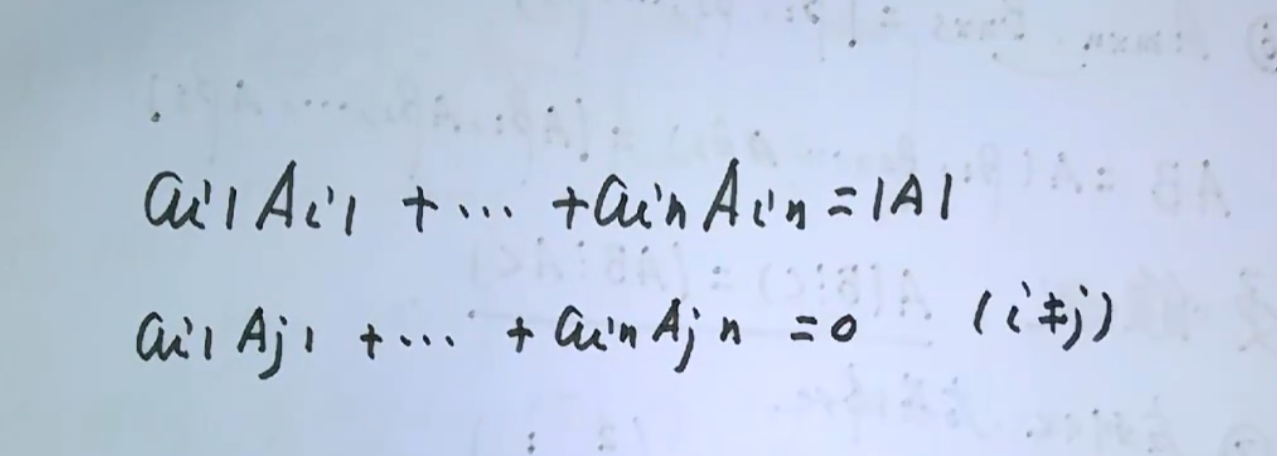
若AA*

若A*A

5逆矩阵理论和秩理论