1逆阵
逆阵只针对方阵
1.1 什么是逆阵

定义法 要求某个矩阵的逆,去配凑出X矩阵 使其相乘为E
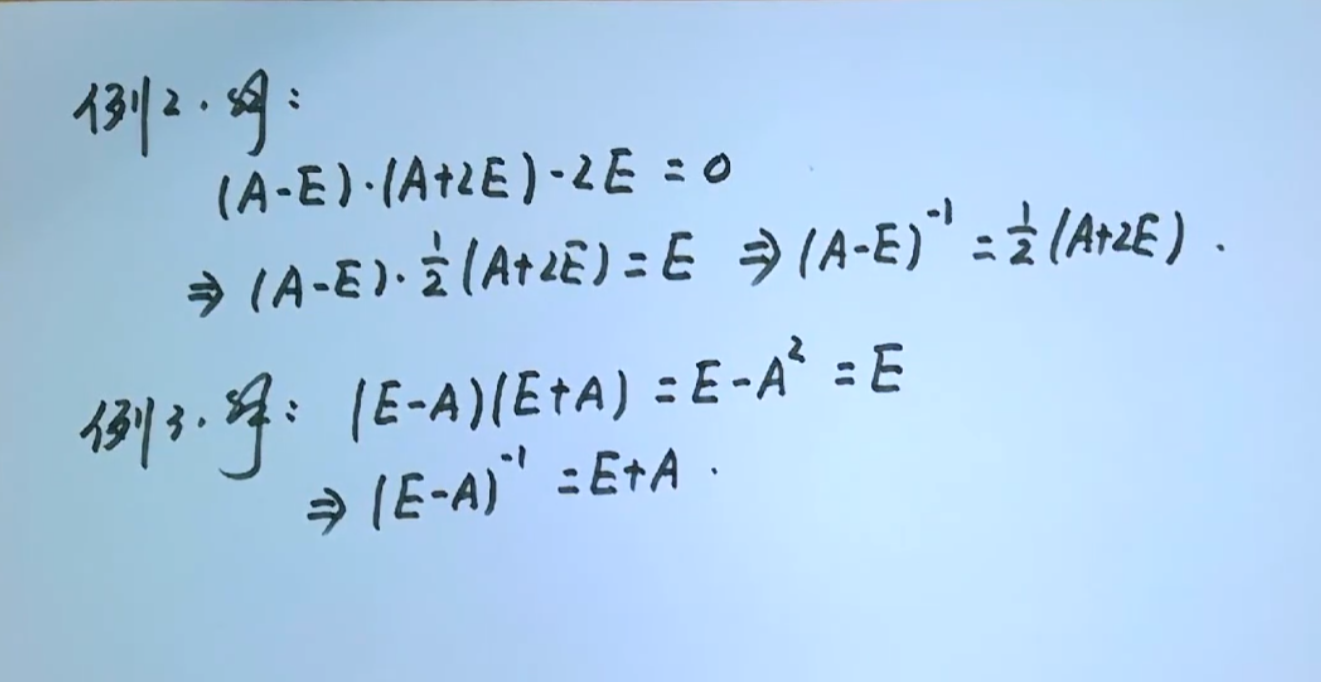
1.2 判断可逆否?
方阵可逆的充要条件 其行列式为0

证明:
根据AB=E 两边同时取行列式,用到拉普拉斯定理 把行列式拿进去 两边均不为0
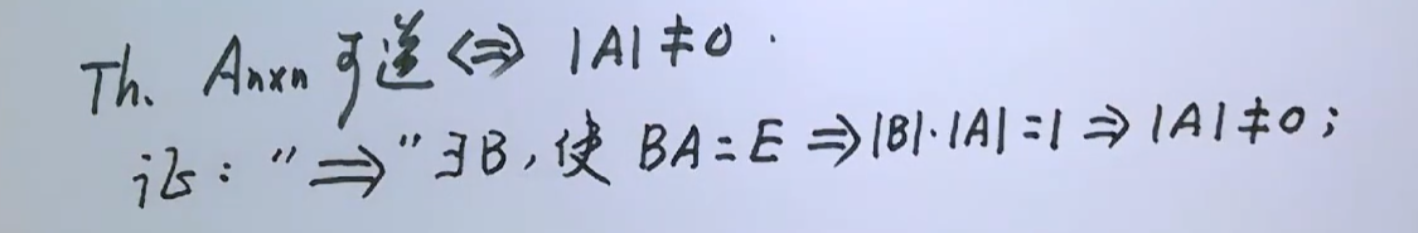
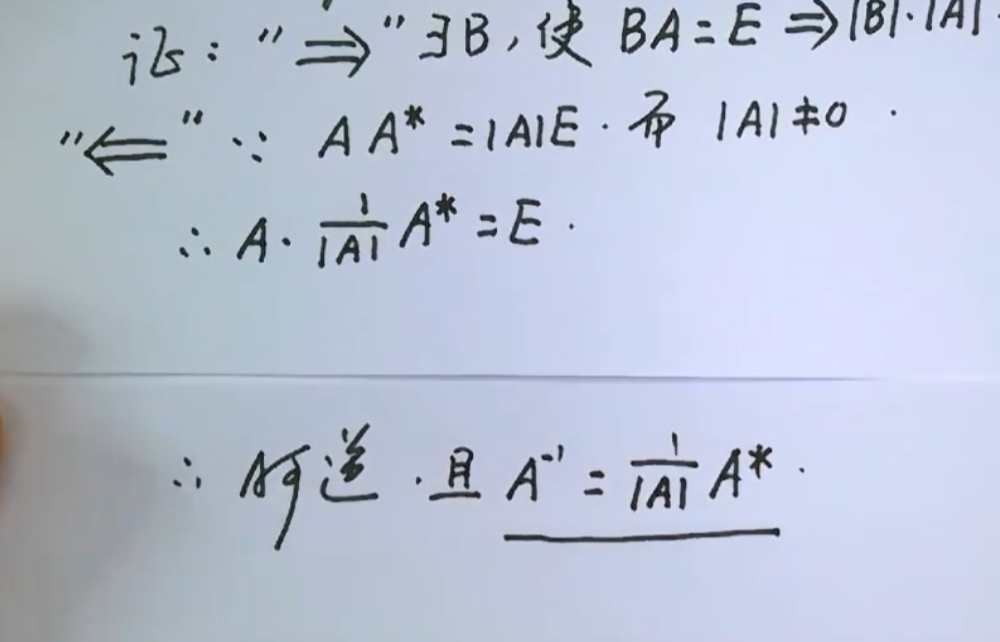
注
$|A^T| =|A|$
$|A^{-1}|=1/|A|$
$|A*|=|A|^{n-1}$
$A是n阶方阵,|kA|=k^n|A|$
$Anxn Bnxn,|AB|=|A||B| Laplace法则$
$((A)^{-1})^{-1}=A$

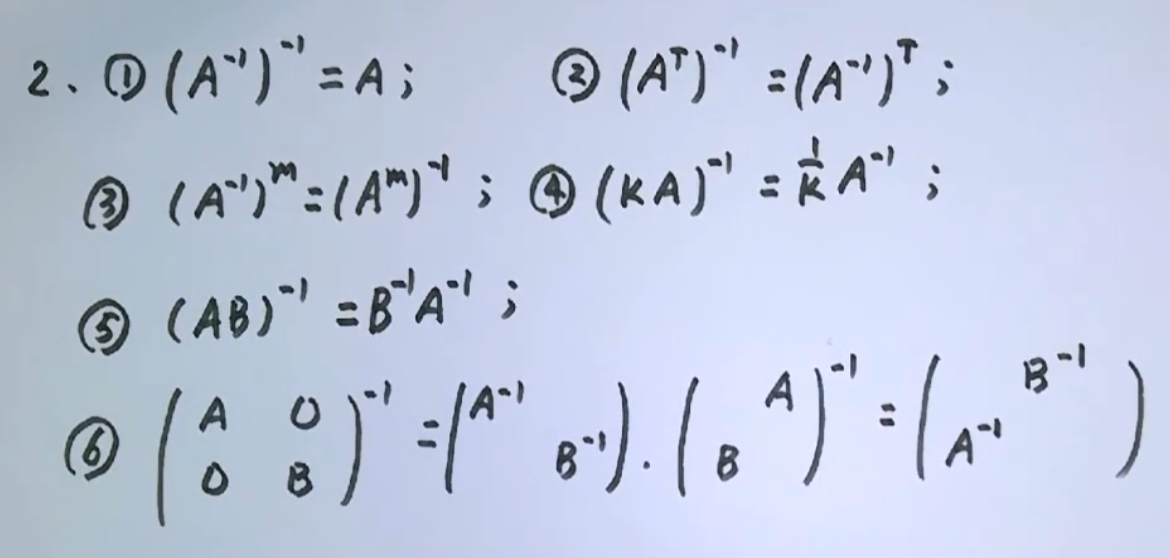
注意方块 副对角线要变换次序
这个公式因为要求了|A|不为0,也即A可逆的时候才可用于求逆矩阵,并且手动求不宜超过三阶,否则计算不现实

A*有方法可以去除
若A可逆 则 $A*=A^{-1}|A|$
根据上面这个重要公式推导出下述
一些常见可推导的公式


1.3 若可逆,求A^{-1}
末尾介绍了三种初等矩阵
I型 对调两行/两列;E(i,j)
II型 某行/列 k倍;Ei(k)
III型 某行/列k倍 加到另行/列;Eij(k) j行k倍加到i行,左乘 ; i列k倍加到j列,右乘。
遵循左行右列



