主成分分析
聚类分析
判别分析 H0
多元正态总体的统计推断 T方检验
1 矩阵代数
1.1定义
1.2矩阵运算
1.3行列式
1.4矩阵的逆
矩阵可逆便 行列式不为0 行列式不为0的矩阵叫非奇异矩阵 行列式为0的矩阵叫奇异矩阵 同时不可逆
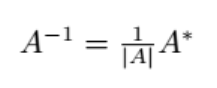

用化最简行阶梯形也可以做
1.5矩阵的秩

1.6特征值,特征向量,矩阵的迹(这三个概念只有方阵才谈




矩阵的迹

1.7正定矩阵和非负定矩阵

顺序主子式
- 从矩阵左上角开始,按顺序取1阶、2阶…n阶的行列式
- k阶顺序主子式是指:取矩阵左上角的k×k个元素构成的行列式


有趣的性质 主对角线的元素的绝对值 一定比该行 该列 所有其余元素绝对值之和还要大
第一章例题







对A(对称矩阵)谱分解,求A特征值特征向量

特征向量要标准化 这就是为什么分母有根号二分之一 本质是除以了(根号下x^2+y^2 这个模长)
为了确保模长为1

2 随机向量
2.1多元分布
2.2数字特征

2.2.1 协方差矩阵

协方差矩阵应用

求解




左上角右下角分别为特征1 和 2 的方差 右上=左下=特征1和2间的相关性


左乘法 类似线性代数
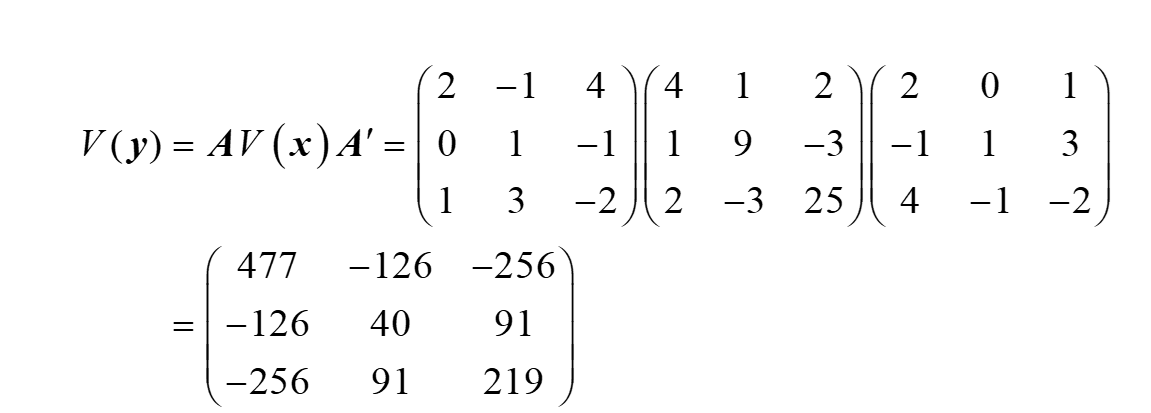
2.3.2 相关矩阵(运用了协方差)



2.3.3 标准化变化
Z-score标准化是一种常用的数据预处理方法,通过将数据转换为零均值和单位方差的新数据集,使得数据符合标准正态分布。其公式为:
$[ z = \frac{x – \mu}{\sigma} ]$

Z-score标准化 归一化后除以标准差


2.3欧氏距离马氏距离



马氏距离有点复杂 求取 一些样本里面 两个样本点的马氏距离


第二章例题


第一问注意联合密度函数性质 在定义域内积分为1 解这个三重积分方程即可 累次积分法 不难
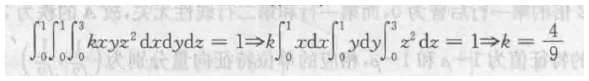
第二问判断xyz是否独立 分别求x y z的边缘密度函数 看fxyz是不是等于fx fy fz 若是 则独立 反之不独立

第三问 如果变量独立 那么条件分布也是边缘密度函数
这三问都需要注意 一定要把定义域包含完整


补充例


求三次偏导为密度
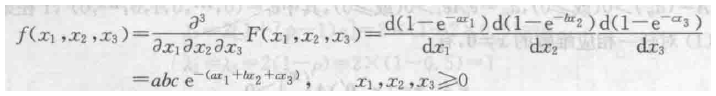

求边缘密度


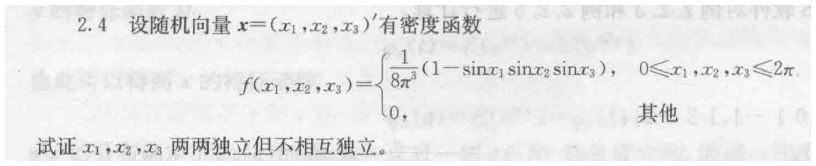
类似第一题 纯计算 求偏导
分布函数F求导得到密度函数
密度函数f积分=1求参数
密度函数f部分积分得到边缘密度函数 边缘密度函数用于判断是否独立 条件分布是用整体密度函数 除以某某条件下那个字母对应的所有密度函数 比如求X在Y=1,Z=2的条件下 就fxyz/fy fz =fx(y=1,z=2)


构造左乘矩阵 然后右乘转置
3 多元正态分布
3.1多元正态分布的定义

3.3极大似然估计及估计量的性质
3.3复相关系数和偏相关系数
第三章题目


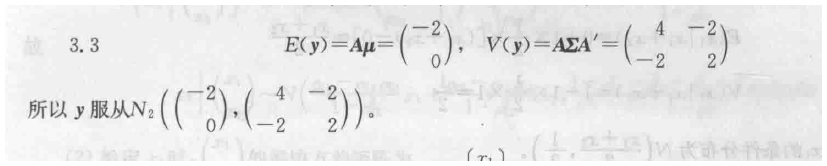
3.3属于 多元正态分布的线性变换问题 均值是左乘变换矩阵即可 协方差矩阵是左乘变换矩阵,同时右乘变换矩阵的转置
前面遇到过

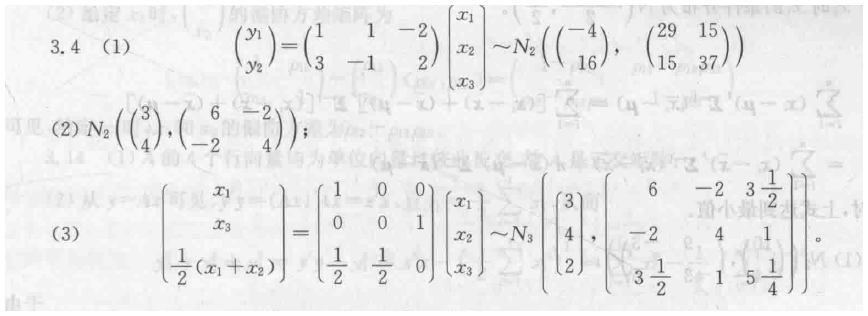
三元正态分布 均值 协方差矩阵
y1和y2构成左乘矩阵 1 1 -2
3 -1 2
类似的 该矩阵左乘均值, 左乘协方差矩阵 然后其转置右乘协方差矩阵 得到线性变换后的联合分布
第一问是左乘行矩阵变换 以及左乘矩阵 右乘转置矩阵协方差矩阵变换
如果学明白了,这三个问题都是用同一种方法解决, 根据条件 构建行变换矩阵 一定可以解决


3.7

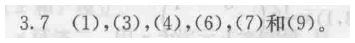

做法很简单 看参数即可 这是协方差的定义 如果rho23=0则x2和x3独立 反之不独立 若rho12和rho13都=0 那么x1和(x2,x3)独立


这个涉及多元正态分布的协方差矩阵里面 参数的含义
3.8 考察多元正态分布 左乘行变换矩阵
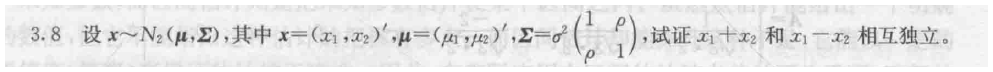

思路很简单,根据行变换矩阵思想 将变换后的sigma矩阵算出来 看rho12 =0 那么就独立
矩阵很简单
1 1
1 -1
如何看多元正态分布的条件分布 这个就是根据概念推导的结果 目前为止 与协方差矩阵一样 需要记住的东西 多元正态分布的条件分布的求解办法

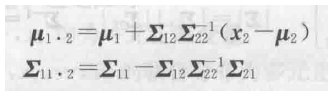

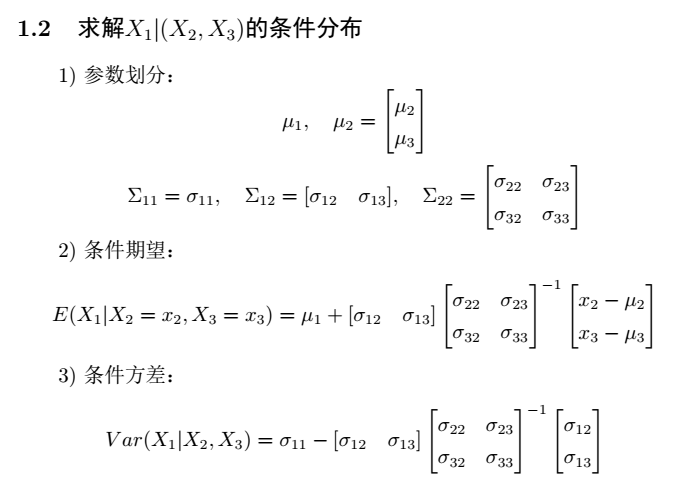
左边X1|(X2,X3)的X1是一维 那么sigma12矩阵一定是1xn维


关键规则:
- Sigma12的维度取决于被解释变量和条件变量的维度
- 行数 = 被解释变量的维度
- 列数 = 条件变量的维度
3.12 有点意思 多元正态分布 边缘分布(行变换) 条件分布 偏相关系数和复相关系数 偏相关系数和复相关系数必须要会条件分布求法才能得到


这个第三问和第四问涉及偏相关系数和复相关系数 有点意思
第一问 x1,x2 均值10,4 sigma 4 -2 ; -2 2 容易
第二问是 多元正态分布的条件分布 已经是比较复杂的形态了 这个主要考察分块矩阵思想和条件分布公式
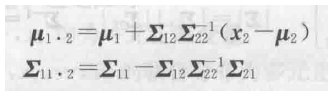
比较复杂的情况是跳一个,例如 (x1,x3)在x2条件下 分块比较麻烦
而(x1,x2)在x3条件下 和x1在(x2,x3)是比较标准的分块 左上角 右下角 即可
分块规则理解了之后 还有一个维度 条件限制的规则 联想 一列是一个限制条件 条件有几个 那么sigma12矩阵就有几列
- Sigma12的维度取决于被解释变量和条件变量的维度
- 行数 = 被解释变量的维度
- 列数 = 条件变量的维度
第三问

第四问

偏相关系数和复相关系数带入公式即可
4 多元正态总体的统计推断
多元正态总体的统计推断总结
1. 两类基本问题
- 单个总体μ的推断
- 多个总体均值向量的比较
2. 单个总体参数推断
- μ的检验
- 已知Σ: T² ~ χ²(p)
- 未知Σ: (n-p)T²/[p(n-1)] ~ F(p,n-p)
- μ的置信区域
- {μ: n(X̄-μ)’S⁻¹(X̄-μ) ≤ c}
- Bonferroni同时置信区间
3. 多个总体均值比较
- 两个总体
- 配对比较:D = X₁-X₂
- 独立样本:合并S矩阵
- 多个总体
- Hotelling’s T²检验
- Wilks’ Lambda统计量
4. 重要统计量
# 检验统计量
T² = n(X̄-μ₀)'S⁻¹(X̄-μ₀) # 未知Σ
T² = n(X̄-μ₀)'Σ⁻¹(X̄-μ₀) # 已知Σ
# 合并协方差
Sp = [(n₁-1)S₁ + (n₂-1)S₂]/(n₁+n₂-2)
# Wilks' Lambda
Λ = |W|/|W+B|5. 关键点
- 样本量要求:n > p
- 正态性假设
- 协方差矩阵是否已知
- 多重比较的校正
4.2单个总体均值的推断

4.3两个总体均值的比较推断

4.5多个总体均值的比较检验(多元方差分析)
4.6协方差矩阵相等性的检验
4.7总体相关系数的检验
第四章例题
4.1 子问题123显著性水平改为alpha=0.01
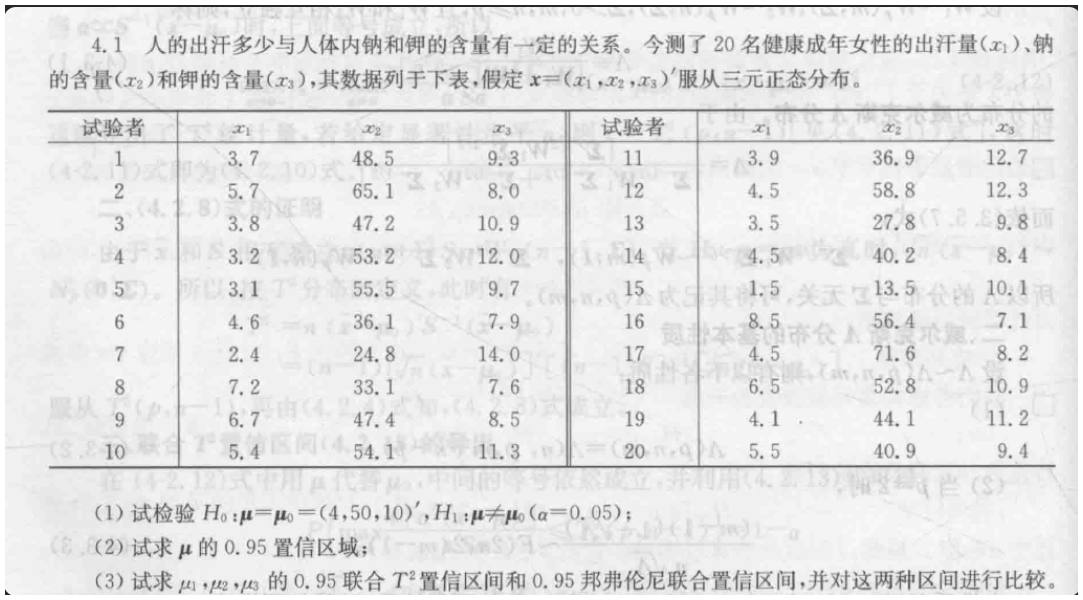



总结 求T^2=n(x均值-预测)’ 协方差矩阵的逆阵 (x均值-预测) 与(p(n-1)/n-p) ( Falpha)
其中x均值-预测值本身是多维的 转置变成1维合理
第二问求置信区间 这个过于复杂,但是原理其实就是t方检验的置信区间
t方检验
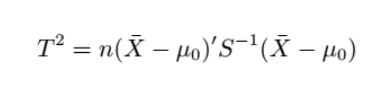
拒绝域就是大于 参数乘以Falpha
置信区间就是小于等于 参数乘以Falpha


第三问
邦弗伦尼区间 略吧


4.2
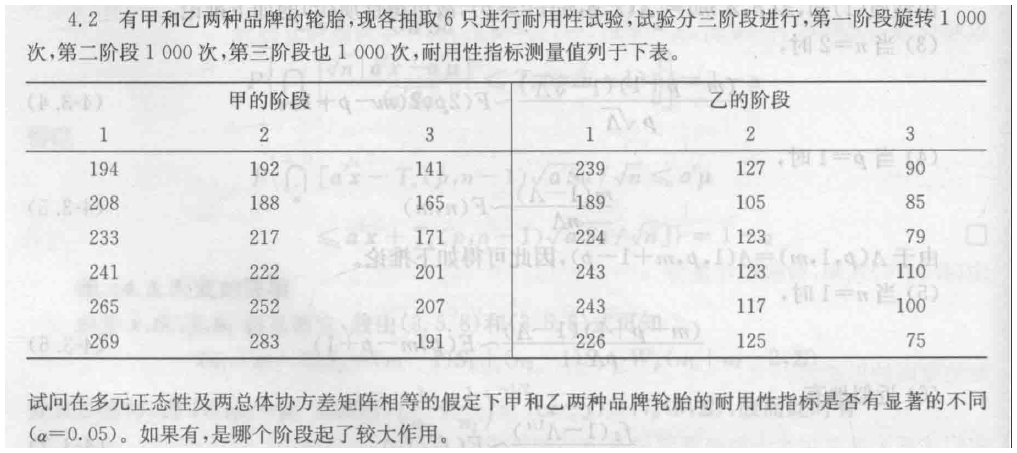
我有甲和乙两种轮胎,各抽6个进行测试,分三个阶段,耐用性指标x1,x2,x3;数据都能得到,现在用t方检验 两种品牌轮胎耐用性是否有显著不同 alpha=0.05 如果有,哪个阶段起了较大作用.请用中文latex输出解法,带字母即可

4.7 alpha=0.1

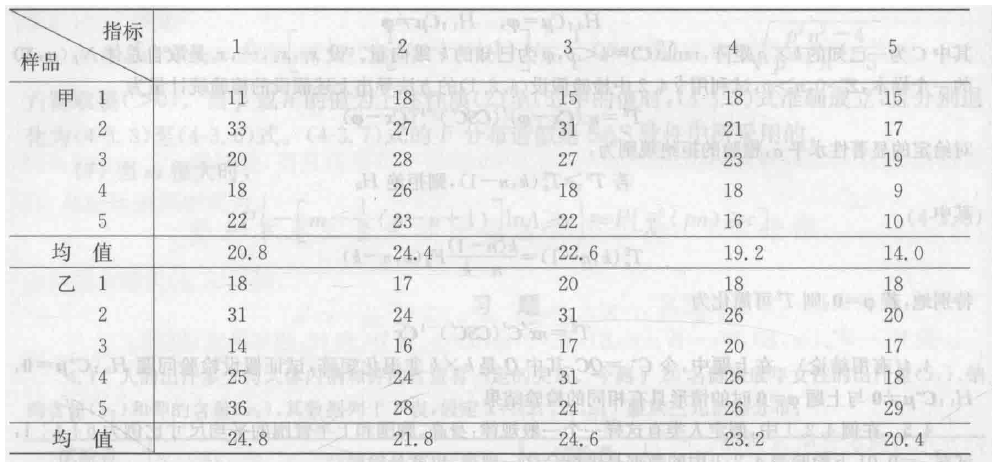
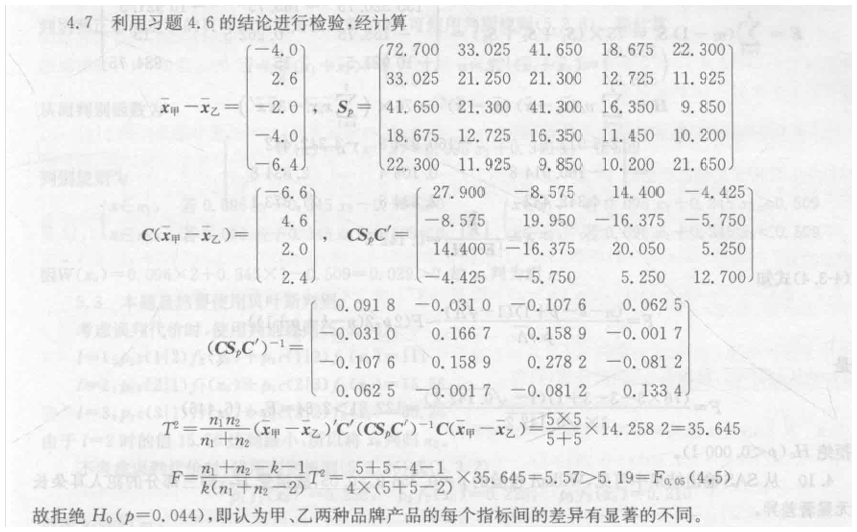
这个用到了二级结论 检验里面嵌套矩阵 过于复杂

4.9 显著性水平改为 α=0.05



4.10 显著性水平改为 a=0.01
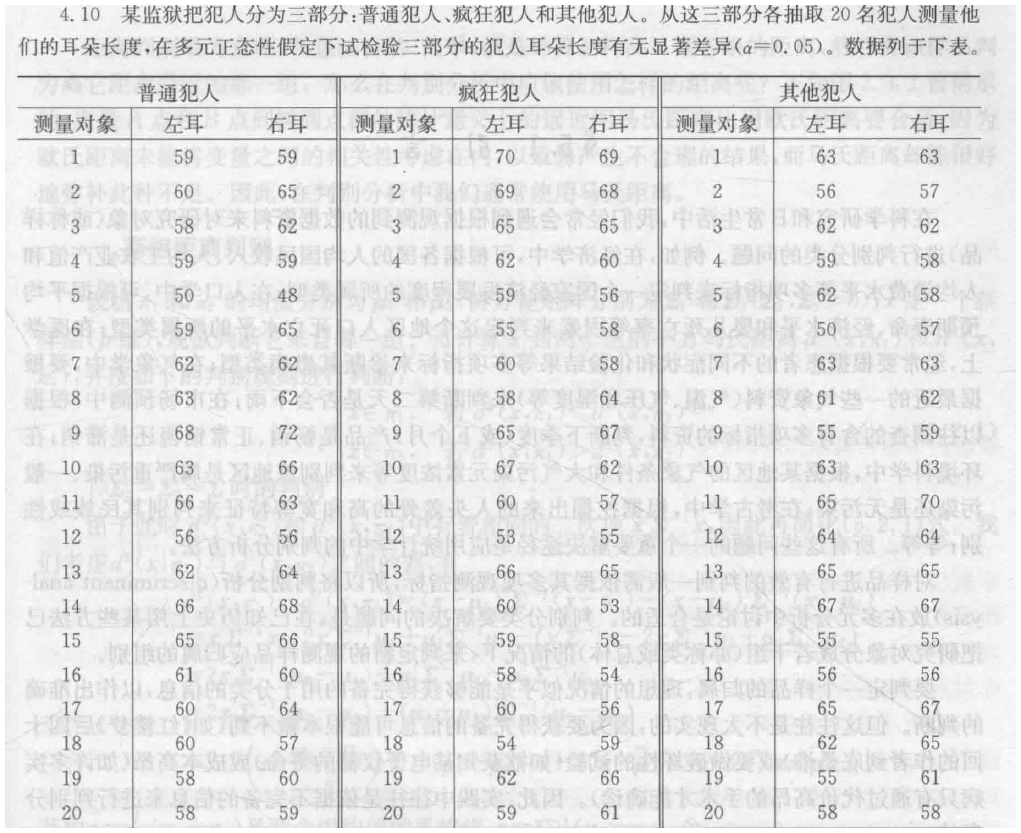
某项产品有三类:A,B,C 每组测量20个数据x1,x2 现在需要检验alpha=0.05下三类产品数据x1,x2有无显著差异,给出中文latex步骤

5 判别分析
距离 费希尔 贝叶斯


5.2距离判别

5.2.1两组距离判别
5.2.2多组距离判别
5.3 贝叶斯判别

5.4 费希尔判别

第五章例题
5.2 Sp改为 Sp=(6.3,1.0; 1.0,8.2)


已知来自组1和组2的两个样本有x1=(4;2)均值 x2=(3;-1)均值 Sp=(6.5 1.1;1.1 8.4)
给出判别规则 将x0=(2;1)分到组1或者组2 假定sigma1=sigma2

5.3 维持不变


先给定三组数据 pi1 pi2 pi3 以及三乘三的误判代价矩阵 给出p1 p2 p3三个先验概率 已知f1x0 f2x0 f3x0的概率密度 如何将样品x0分到三个组中的一个,考虑误判代价和不考虑误判代价的两种做法?
5.5 子问题(2)(3)中 先验概率改为 p1=0.4,p2=0.6
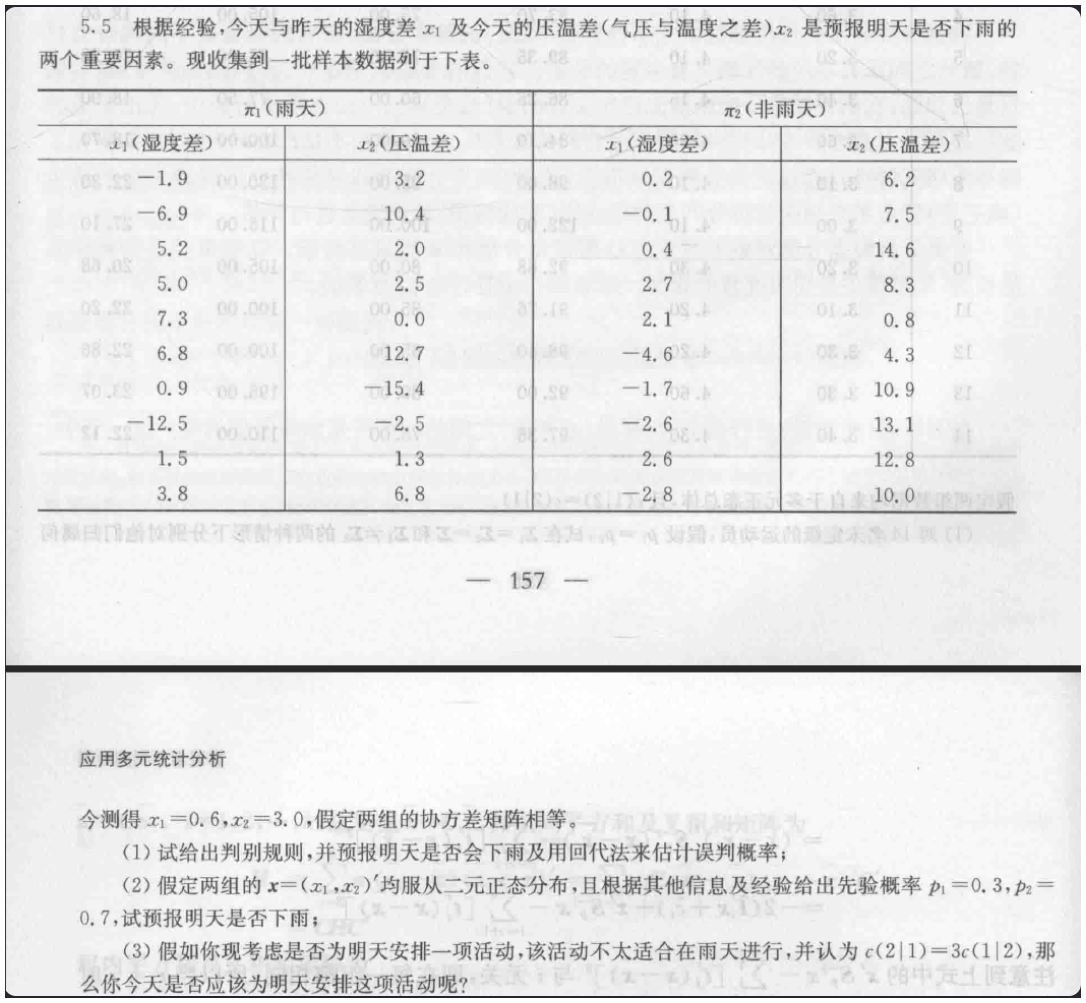

已知pi1 雨天 pi2非雨天 pi1和pi2都是两维x1 x2 ;现在有先验概率p1 p2 x0=(x1,x2) 我需要预报明天是否下雨.用贝叶斯判别怎么做


5.6 子问题(3)中 先验概率改为 p1=0.7,p2=0.3
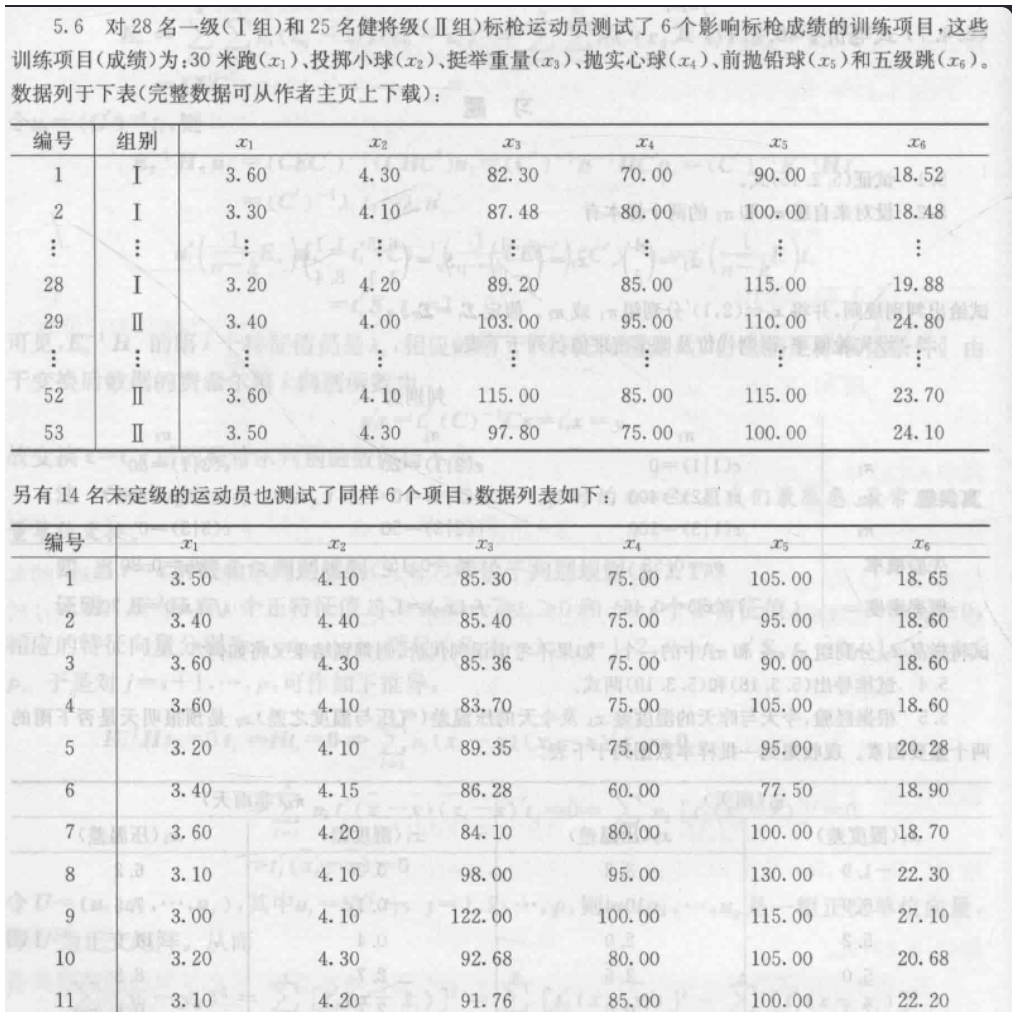


5.8 只需给出费希尔判别函数
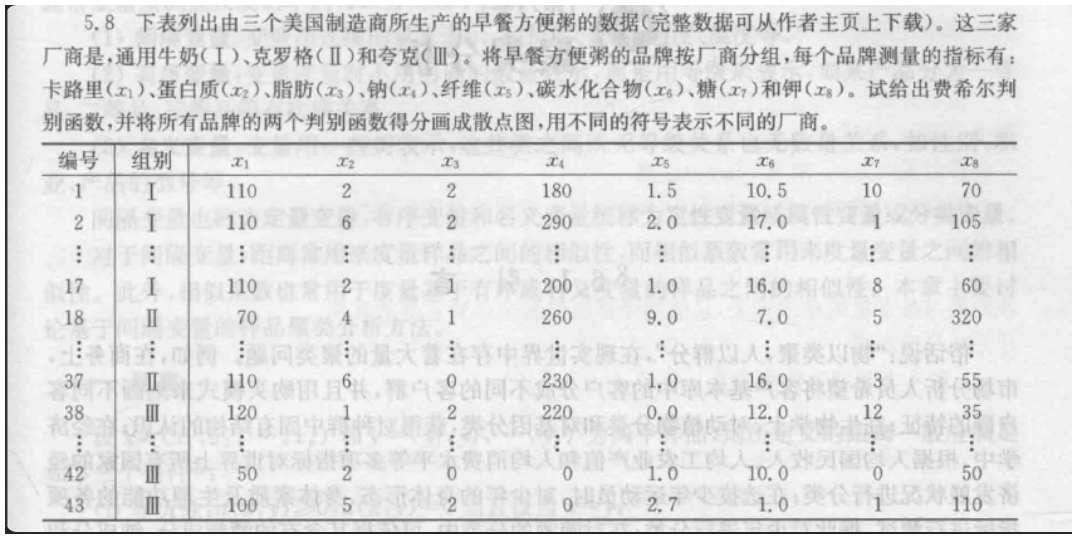

6 聚类分析
6.2 距离和相似系数
6.3 系统聚类法
6.4 动态聚类法

聚类分为系统聚类法和动态聚类法 动态聚类法计算量要比建立在距离矩阵基础上的系统聚类法要小得多
最短距离法 每次找全局最小的两个距离,将其合并,(合并后的与其他的再进行计算距离) 每次合并全局最小两个距离


第六章题目
6.2

6.3




6.5
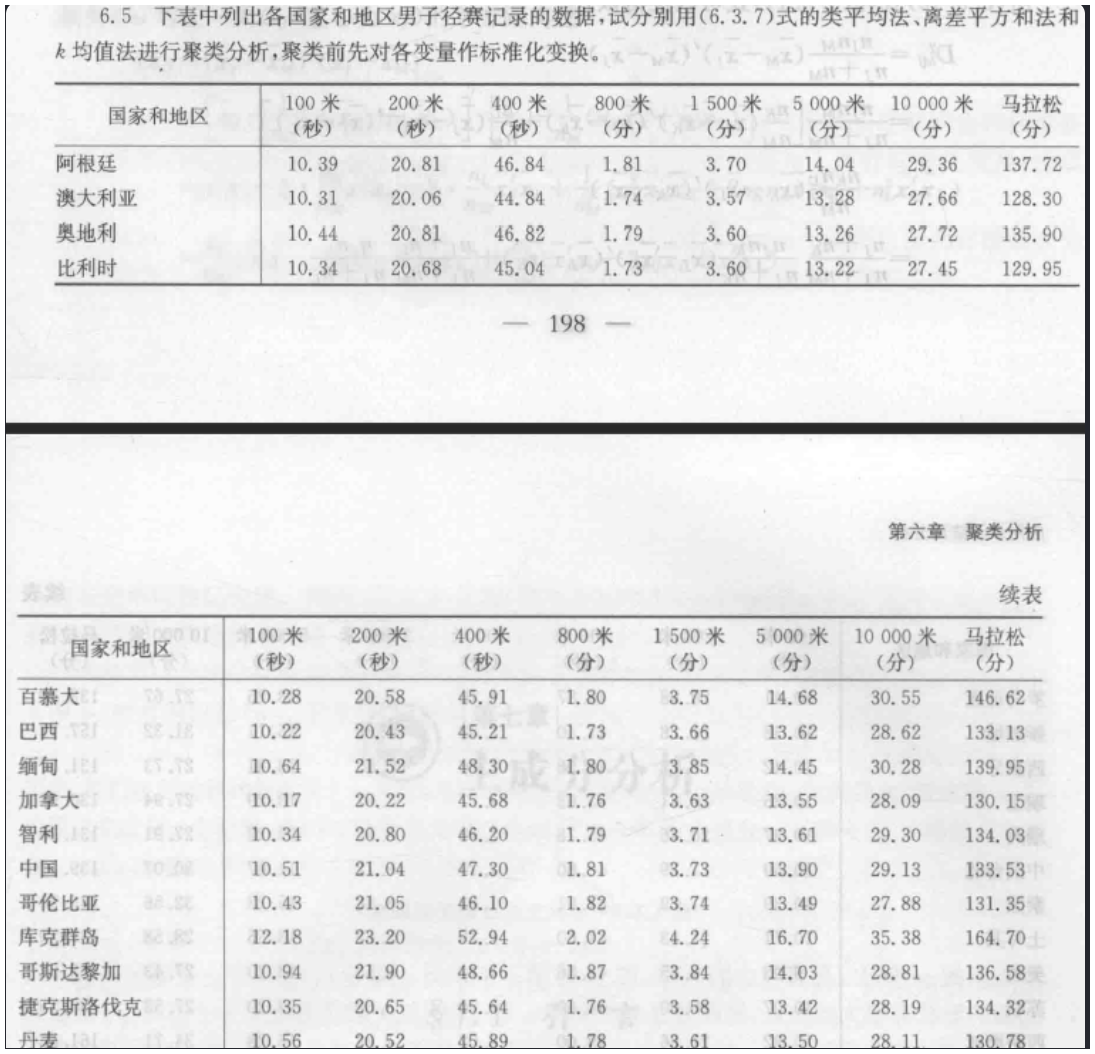
7 主成分分析

7.2 总体的主成分
7.3 样本的主成分
7.4 若干补充及应用中需注意的问题
第七章题目
7.1
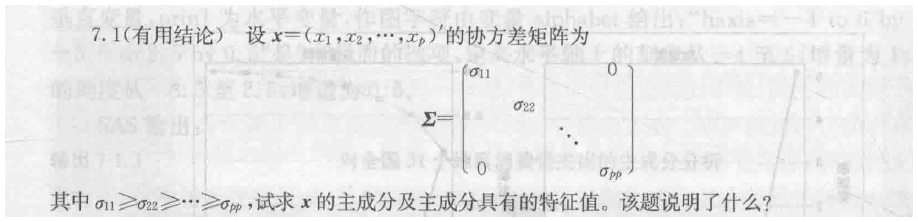
当原始变量互不相关的时候 主成分为原始变量 此时进行主成分分析什么也得不到
7.4

7.5

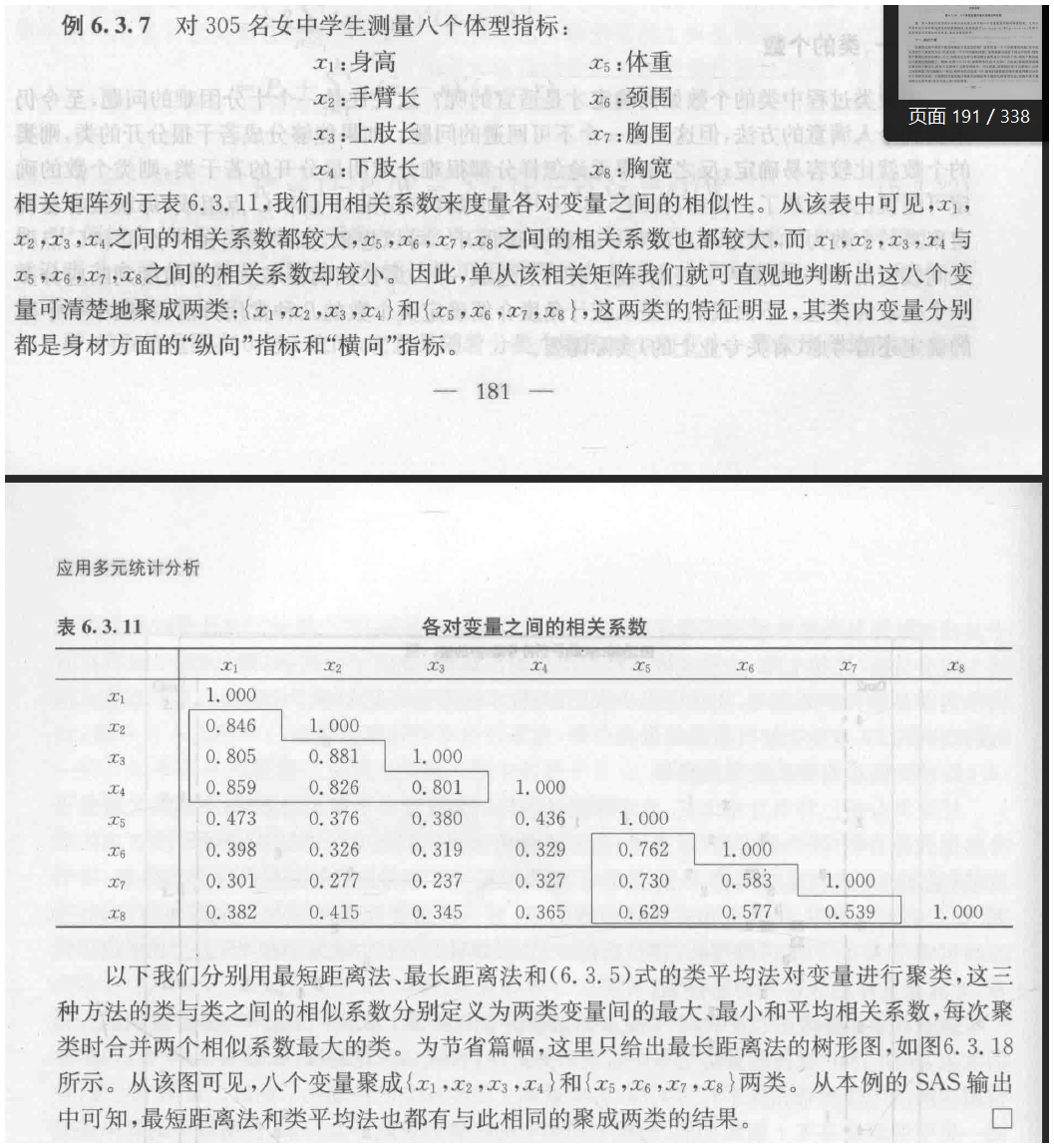
7.6
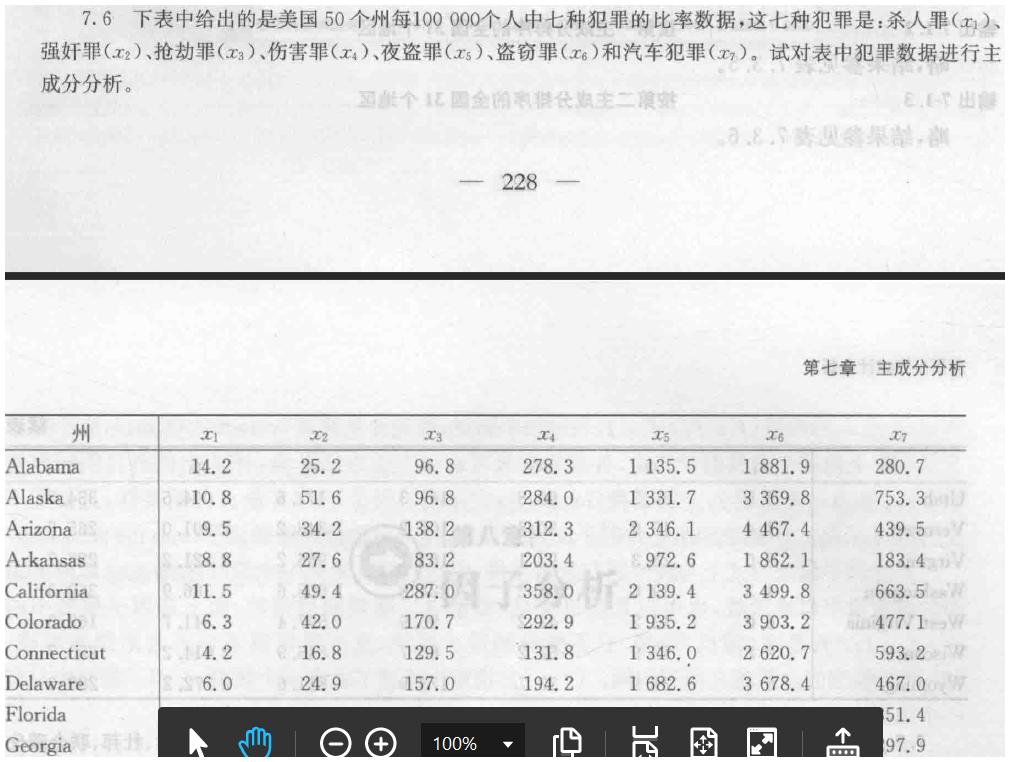
8 因子分析
1. 因子分析
降维特点:
- 将p个原始变量降为m个因子(m < p)
- 通过因子载荷矩阵实现降维
- 保留原始数据主要信息

8.2 正交因子模型
- 将p个观测变量表示为m个相互正交的公共因子的线性组合(m < p)
- 降维的同时保持原始数据的主要信息
8.3 参数估计

8.4 因子旋转
8.5 因子得分
第八章题目
8.4
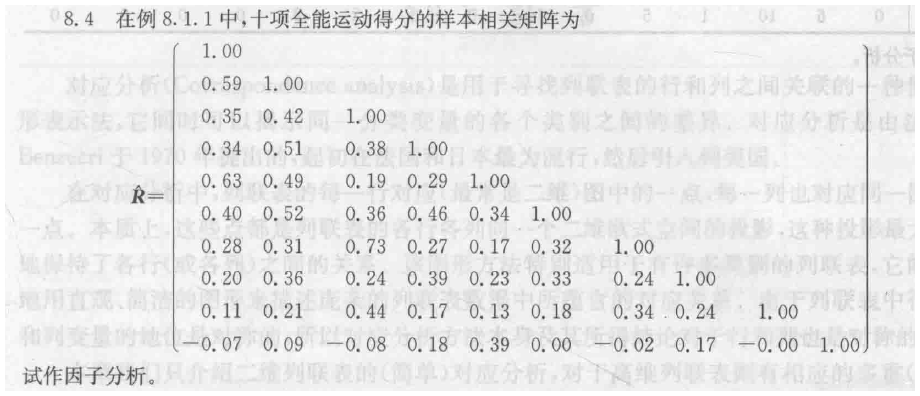
8.5
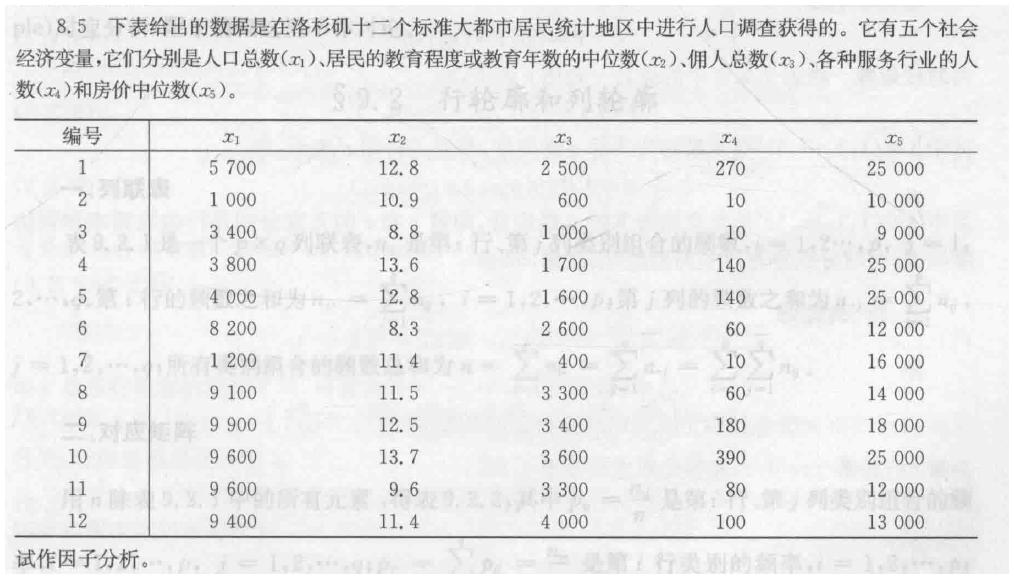
8.6
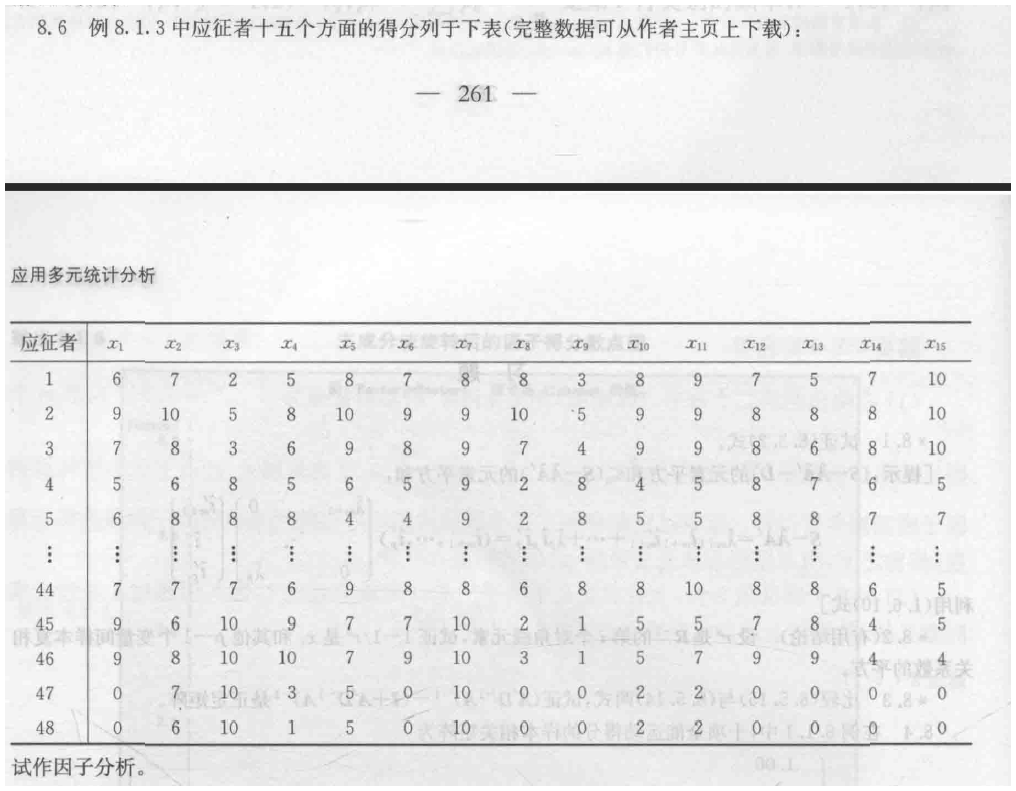
9 对应分析
降维特点:
- 将列联表数据转化为低维图形显示
- 通过奇异值分解实现降维
- 保持行列类别间关联关系


9.2 行轮廓和列轮廓
9.3 独立性的检验和总惯量
9.4 行,列轮廓的坐标
9.5 对应分析图
第九章题目
9.1

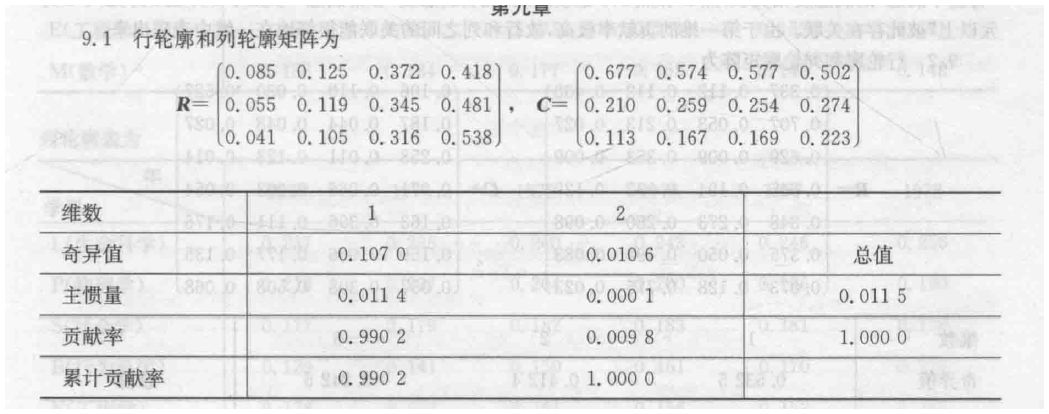


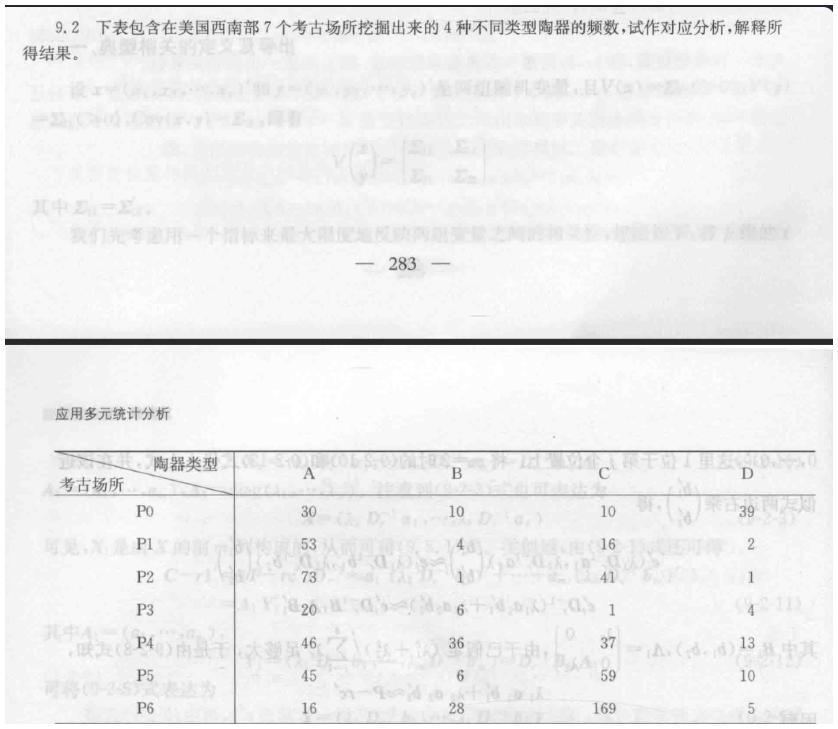
9.2
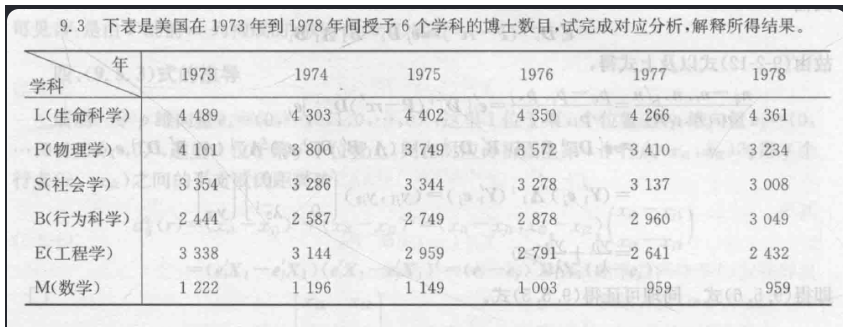
9.3
10 典型相关分析
降维特点:
- 将两组变量降维为几对典型变量
- 通过特征值分解实现降维
- 保持两组变量间最大相关性
典型相关分析的核心问题
主要解决的问题:
- 研究两组变量之间的相关关系
- 寻找两组变量的最佳线性组合
10.2 总体典型相关
10.3 样本典型相关
10.4 典型相关系数的显著性检验


第十章题目
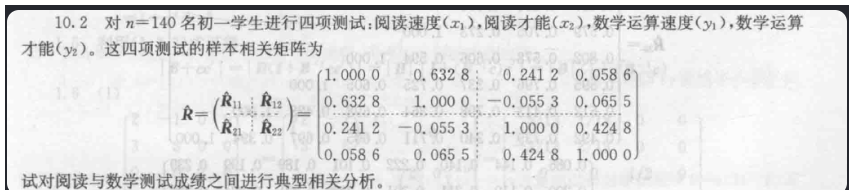
10.2

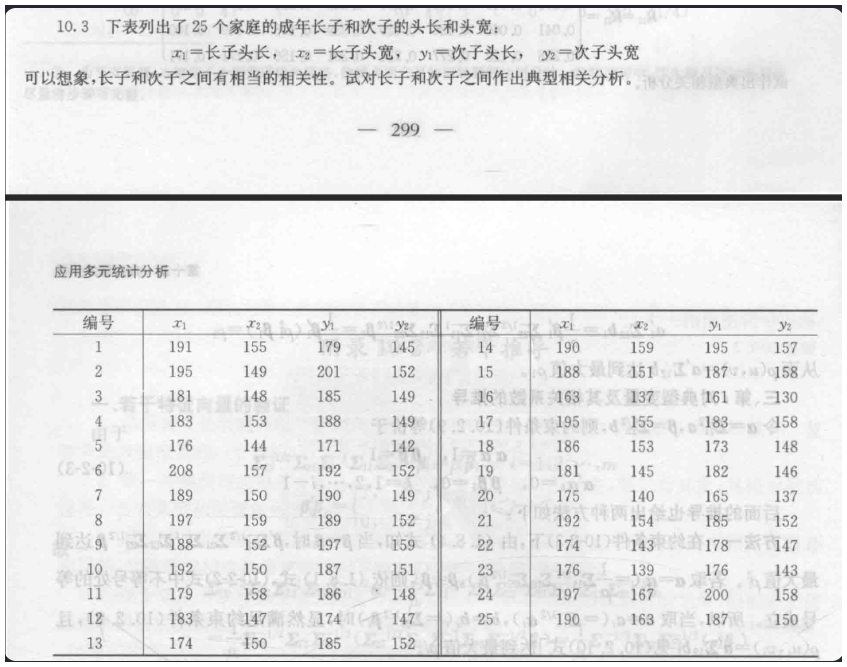
10.3
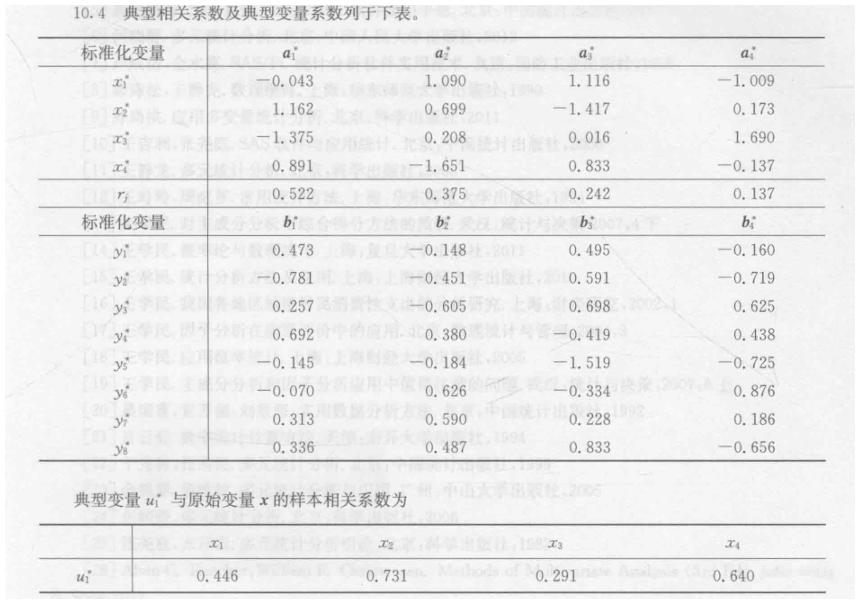
10.4


有这几个章节:4多元正态总体的统计推断;5判别分析;聚类分析;7主成分分析;8因子分析;9对应分析;10典型相关分析.如果让你出6道计算大题,在试卷上,允许学生用计算器.出什么能考察学生能力的同时,又不会因为计算过于费时导致副作用?
开干
多元正态总体的T²检验
某产品有两组样本(n₁=n₂=10),测量3个指标:
组1均值:(2,3,1)
组2均值:(3,2,2)
合并协方差矩阵S已知(给出3×3矩阵,数值简单)
要求:
(1) 在α=0.05下检验两总体是否有显著差异
(2) 计算置信区间
- 组1均值:$\bar{X}_1 = (2, 3, 1)$
- 组2均值:$\bar{X}_2 = (3, 2, 2)$
- 合并协方差矩阵: [ S = \begin{pmatrix} 1 & 0.5 & 0.3 \ 0.5 & 1 & 0.4 \ 0.3 & 0.4 & 1 \end{pmatrix} ]
判别分析
有三组二维数据各4个样本:
组A:(1,2),(2,3),(1,1),(2,2)
组B:(4,5),(5,4),(5,5),(4,4)
组C:(7,8),(8,7),(8,8),(7,7)
要求:将新样本(3,3)判别分类
系统聚类分析
给出5个样本的2维数据,数值简单:
(1,1),(2,2),(5,5),(6,6),(7,7)
要求用最短距离法进行聚类,画出谱系聚类图
主成分分析
给出3×3相关矩阵R(数值简单),求:
(1) 主成分及其方差贡献率
(2) 解释主成分的实际含义
因子分析
给出4×4相关矩阵(数值简单),要求:
(1) 提取2个公共因子
(2) 计算因子载荷矩阵
(3) 进行正交旋转
对应分析
某单位对100名员工进行满意度调查,按年龄(A1:20-30岁,A2:31-40岁,A3:41-50岁)和
满意度级别(B1:很满意,B2:基本满意,B3:不满意)统计得到列联表N:
B1 B2 B3A1 20 15 5
A2 10 25 5
A3 5 10 5
要求:
- 计算对应表P
- 求行轮廓矩阵和列轮廓矩阵
- 计算第一维的贡献率
- 解释结果含义
典型相关分析
两组变量(各2个)的相关矩阵已知,要求:
(1) 求第一对典型变量
(2) 计算典型相关系数
(3) 进行显著性检验