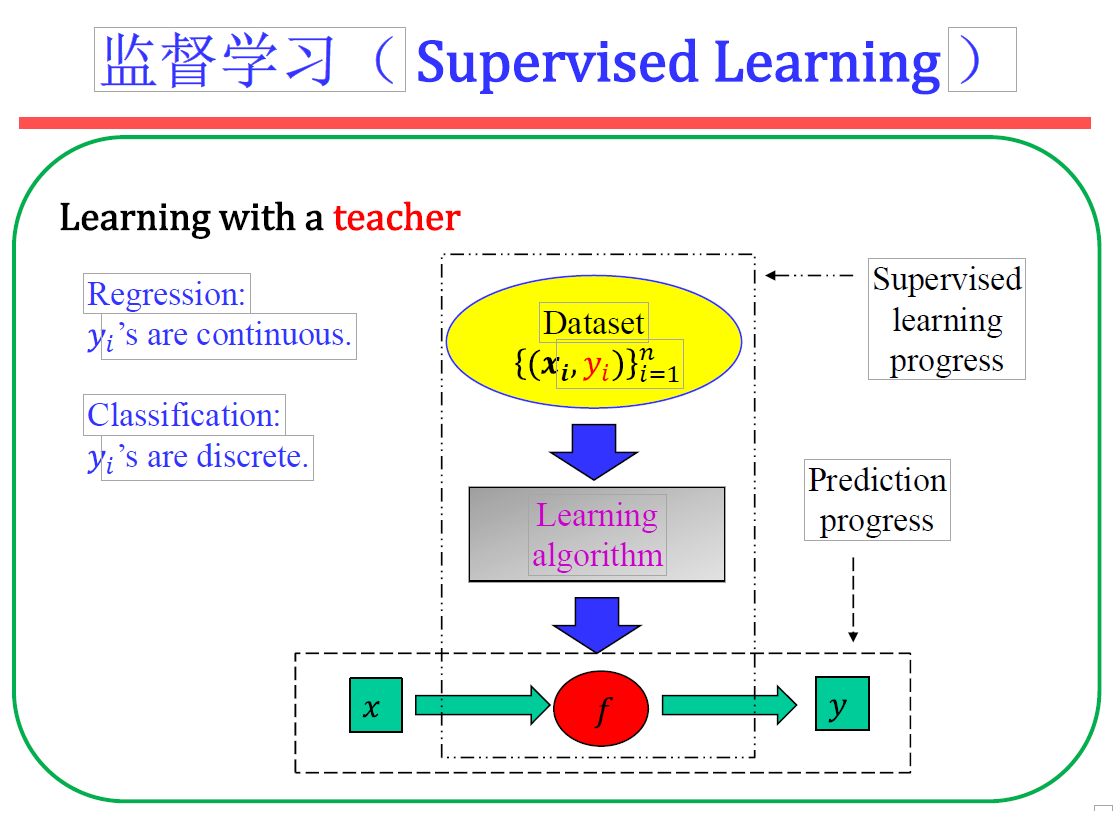
0、前期准备
配置anaconda3的环境变量
使用anaconda3 作为python包管理器,把包都存在统一集成环境中,后续在IDE中使用anaconda3的python解释器即可
在创建项目时,使用已有conda的python解释器
1、实现线性回归算法
自己构造数据集

1.1、代码
import numpy as np
import matplotlib.pyplot as plt
# 设置中文字体,否则图片上的中文会显示成方框
plt.rcParams['font.sans-serif'] = ['SimHei'] # 使用黑体
plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题
import time
# 生成人工线性数据
np.random.seed(0)
x = np.random.rand(100) * 10 # 100个随机点,范围在 [0, 10]
y = 3 * x + 7 + np.random.randn(100) # 带有噪声的线性关系
# 方法1:使用公式1
start_time = time.time()
x_mean = np.mean(x)
y_mean = np.mean(y)
w1 = np.sum((x - x_mean) * (y - y_mean)) / np.sum((x - x_mean)**2)
w0 = y_mean - w1 * x_mean
print(f"方法1: w1 = {w1}, w0 = {w0}")
time_method_1 = time.time() - start_time
# 方法2:使用正规方程
start_time = time.time()
X = np.vstack([np.ones(len(x)), x]).T
w = np.linalg.inv(X.T @ X) @ X.T @ y
print(f"方法2: w = {w}")
time_method_2 = time.time() - start_time
# 比较运行时间
print(f"方法1的时间: {time_method_1}")
print(f"方法2的时间: {time_method_2}")
# 绘制结果
plt.scatter(x, y, label='数据点')
plt.plot(x, w1 * x + w0, color='red', label='方法1的拟合线')
plt.plot(x, X @ w, color='blue', linestyle='--', label='方法2的拟合线')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
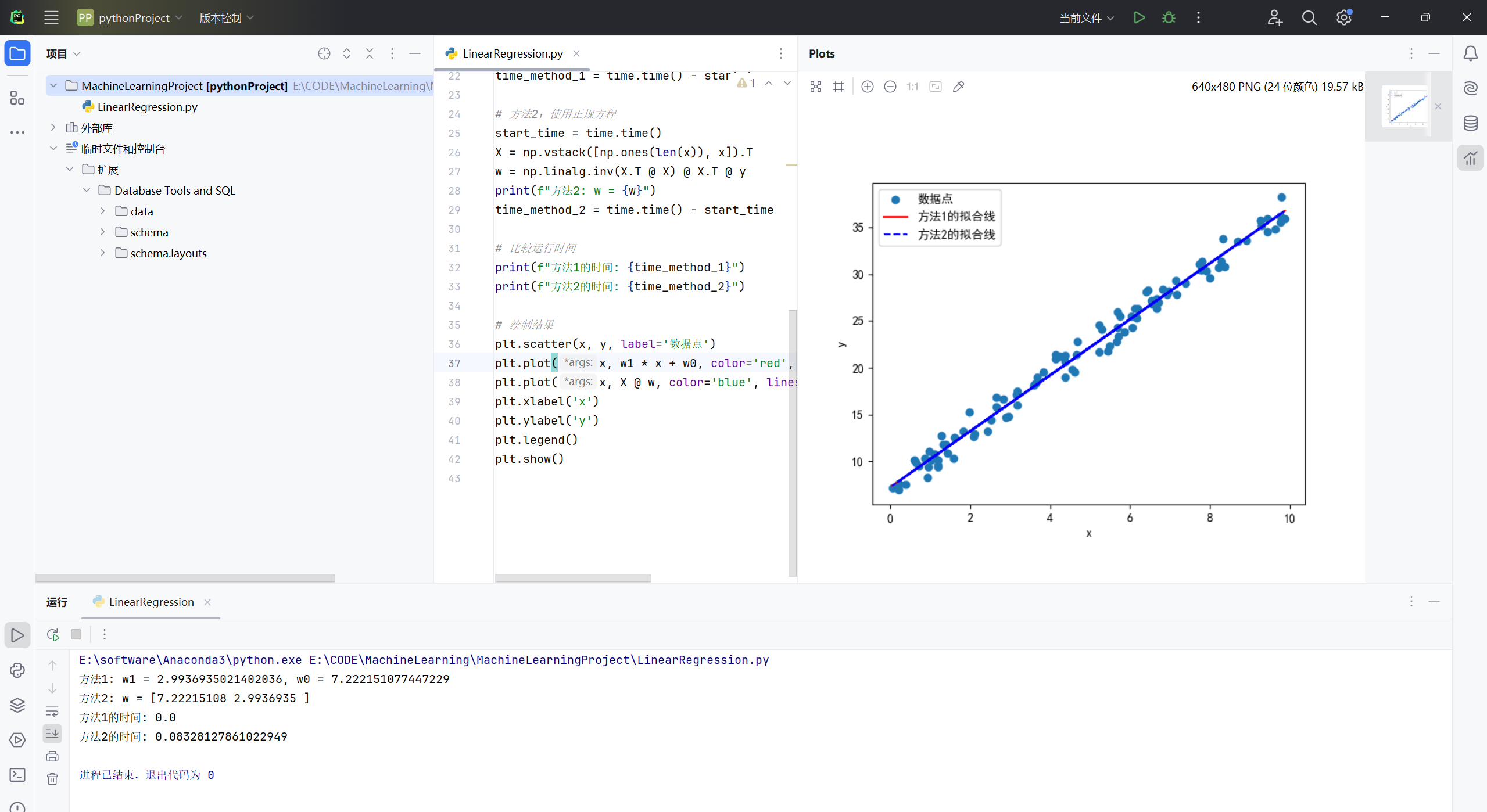
plt.show()1.2、分析
方法1和2得到的拟合线几乎重合,时间相差无几
2、用 LogisticRegression对数几率回归模型做分类任务
自己找数据集或自己构建数据集,需要画图,得到某种度量结果,如准确率、召回率、F1值等。
2.1、代码
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, recall_score, f1_score
from sklearn.model_selection import train_test_split
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei'] # 使用黑体
plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题
# 生成数据集
np.random.seed(0)
num_samples = 200
X = np.random.randn(num_samples, 2)
y = (X[:, 0] + X[:, 1] > 0).astype(int)
# 数据可视化
plt.scatter(X[y == 0][:, 0], X[y == 0][:, 1], color='red', label='Class 0')
plt.scatter(X[y == 1][:, 0], X[y == 1][:, 1], color='blue', label='Class 1')
plt.legend()
plt.title("数据分布")
plt.show()
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
# 构建和训练模型
model = LogisticRegression()
model.fit(X_train, y_train)
# 预测
y_pred = model.predict(X_test)
# 计算度量结果
accuracy = accuracy_score(y_test, y_pred)
recall = recall_score(y_test, y_pred)
f1 = f1_score(y_test, y_pred)
print(f"准确率: {accuracy:.2f}")
print(f"召回率: {recall:.2f}")
print(f"F1值: {f1:.2f}")
# 结果可视化
xx, yy = np.mgrid[X[:, 0].min():X[:, 0].max():.01, X[:, 1].min():X[:, 1].max():.01]
grid = np.c_[xx.ravel(), yy.ravel()]
probs = model.predict_proba(grid)[:, 1].reshape(xx.shape)
plt.contourf(xx, yy, probs, 25, cmap="RdBu", alpha=.8)
plt.scatter(X[y == 0][:, 0], X[y == 0][:, 1], color='red', label='Class 0')
plt.scatter(X[y == 1][:, 0], X[y == 1][:, 1], color='blue', label='Class 1')
plt.legend()
plt.title("决策边界")
plt.show()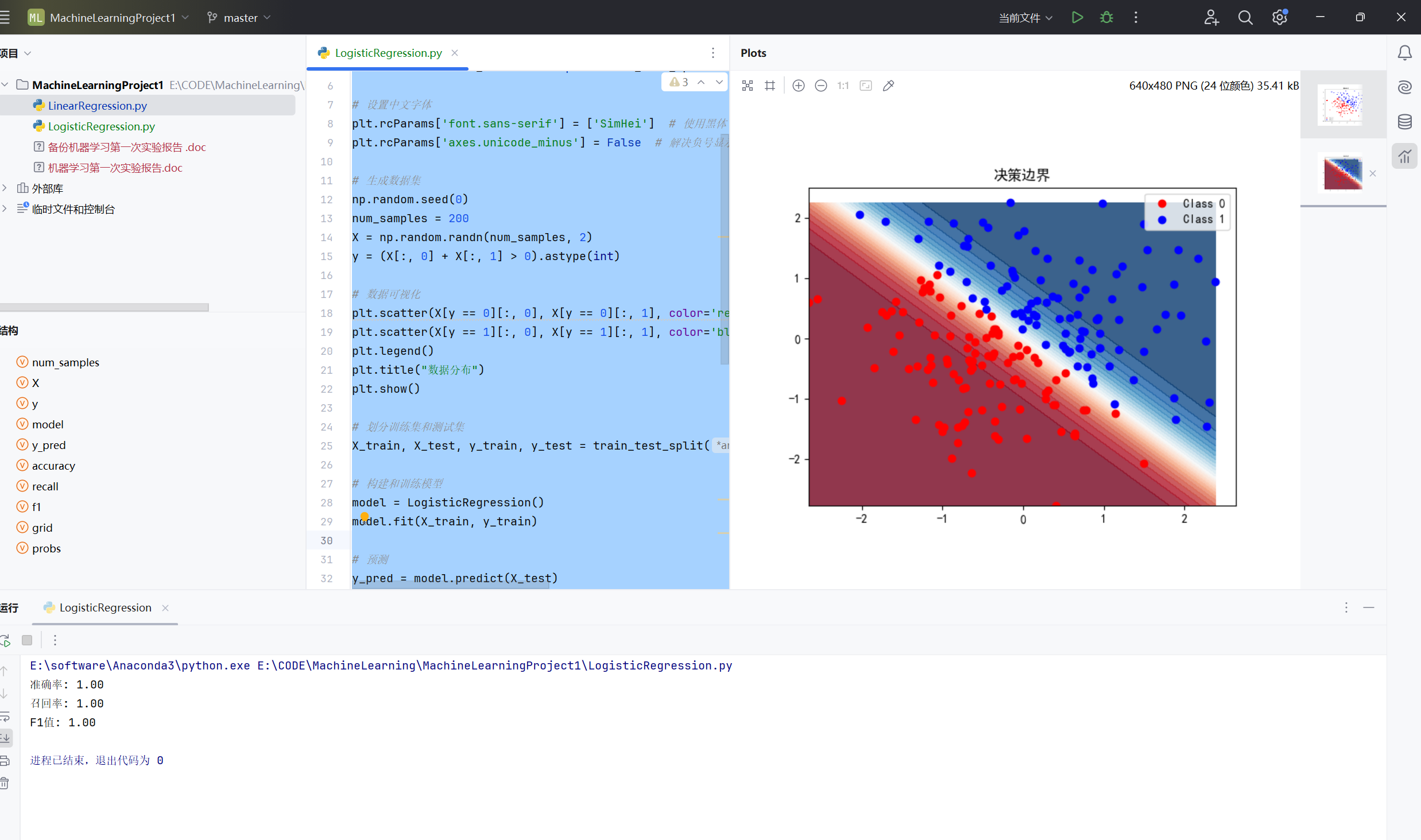
2.2、分析
在这个代码片段中,准确率、召回率和 F1 值都为 1 的原因可能是数据集非常简单且线性可分。
- 数据生成:
np.random.seed(0) num_samples = 200 X = np.random.randn(num_samples, 2) y = (X[:, 0] + X[:, 1] > 0).astype(int)生成的数据集是二维的,并且标签是通过判断两个特征之和是否大于 0 来生成的。这意味着数据是线性可分的。 - 模型训练:
model = LogisticRegression() model.fit(X_train, y_train)对数几率回归模型非常适合处理线性可分的数据集。在这种情况下,模型能够完美地找到分离两类数据的决策边界。 - 预测和评估:
python y_pred = model.predict(X_test) accuracy = accuracy_score(y_test, y_pred) recall = recall_score(y_test, y_pred) f1 = f1_score(y_test, y_pred)
由于数据集是线性可分的,模型在测试集上的预测结果将会非常准确,所有的预测都将是正确的。因此,准确率、召回率和 F1 值都为 1。
如果使用更复杂或非线性的数据集,模型的性能指标可能会有所不同。
备注
精确率(查准率)- Precision
所有被预测为正的样本中实际为正的样本的概率,公式如下:
精准率 =TP/(TP+FP)
召回率(查全率)- Recall
实际为正的样本中被预测为正样本的概率,其公式如下:
召回率=TP/(TP+FN)
F1
F1=(2×Precision×Recall)/(Precision+Recall)
$F1=\frac{2*查准率*查全率}{查准率+查全率}$