1 绪论
1.1基本概念
1.2NLP发展历史
1.3NLP研究内容
1.4NLP基本问题
1.5NLP面临的困难
1.6NLP基本研究方法
2 NLP前置数学基础
2.1 概率论基础
2.1.1概率
2.1.2 条件概率
2.1.3 贝叶斯公式
2.1.4 期望
2.1.5 二项分布
2.1.6 激活函数
2.1.7 最大似然估计
2.1.8 梯度下降
2.2 信息论基础
2.2.1 熵 entropy


2.2.2 联合熵
2.2.3 条件熵
2.2.4 熵的连锁反应
2.2.5 熵率
2.2.6 互信息
2.2.7 互信息与熵的关系
2.2.8 相对熵
2.2.9 交叉熵
2.2.10语言与其模型的交叉熵
2.2.11 迷惑度(困惑度 Perplexity)

我们一般要找困惑度最小的模型 (本质上就是交叉熵 )
2.2.12 噪声信道模型
信息在传输过程中可能受到干扰,为了描述这种干扰,创造出一个噪声信道模型

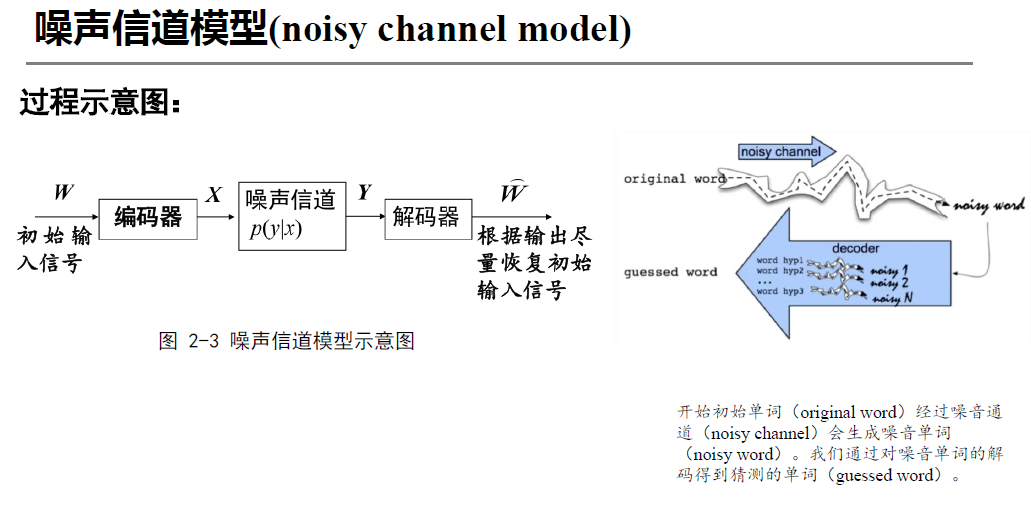
一个常见的噪声信道模型是加性高斯白噪声信道(AWGN Channel, Additive White Gaussian Noise),其基本结构如下:
- 信息源:这是原始的消息或信号,通常是数字信号或模拟信号。
- 编码器:为了增加信号在传输中的可靠性,编码器会将信息源进行编码,例如进行误差检测和纠正。
- 信道:信号通过一个可能带有噪声的传输媒介传输。噪声通常被假设为加性白噪声,这种噪声具有零均值和常数方差,且在不同频率下功率谱密度是均匀的。
- 噪声:信号在传输过程中会受到噪声的干扰,噪声通常用一个随机变量来表示,可能是高斯分布的,也可能是其他类型的噪声(如泊松噪声、脉冲噪声等)。
- 解码器:接收到的信号通过解码器恢复原始信息。如果噪声较强,信号可能会出现错误,解码器需要采用一些策略来减少错误。
4 语料库与语言知识库
4.1 语料库/语料库语言学的基本概念
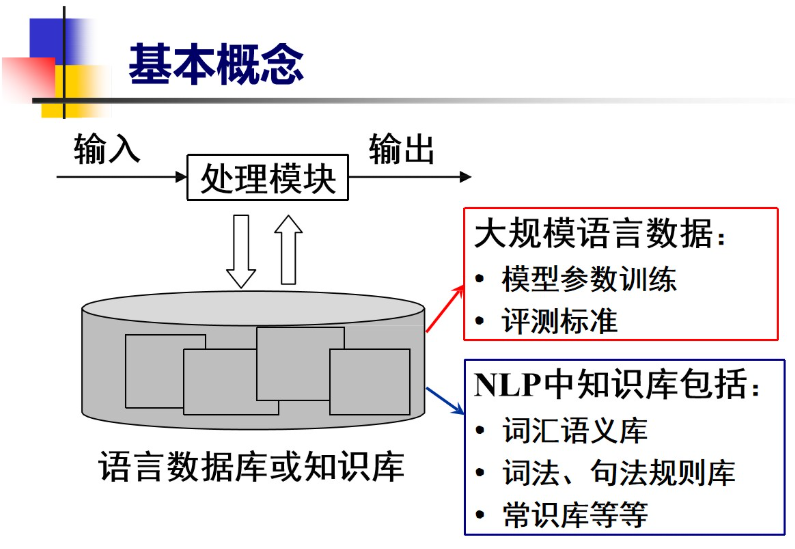

4.2 研究内容和发展历程

发展历程



1950前 早期
1957-1980 沉寂
1980-至今 复苏发展
4.3 语料库类型
4.3.1 按语言种类 是否有标注划分语料库
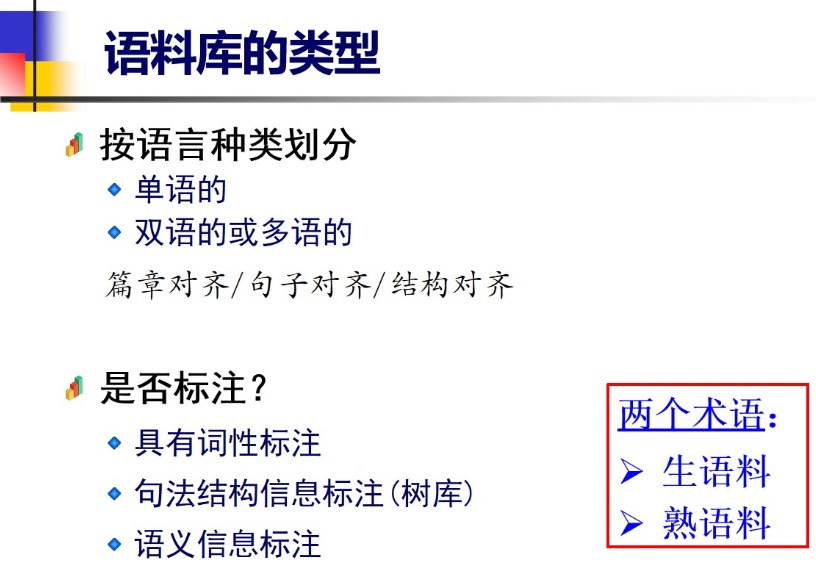
4.3.2 平衡语料库

4.3.3 平行语料库


4.3.4 共时语料库与历时语料库

4.4 典型语料库
常用到的
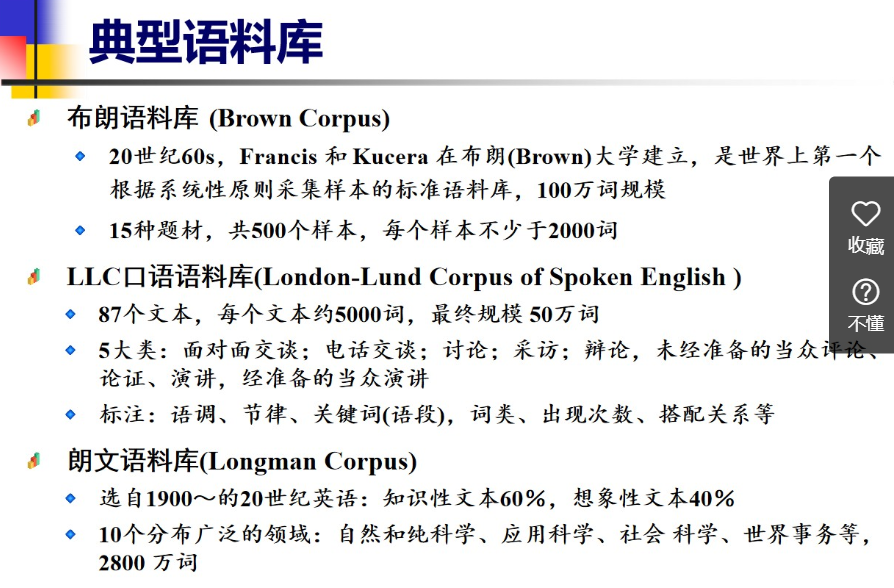

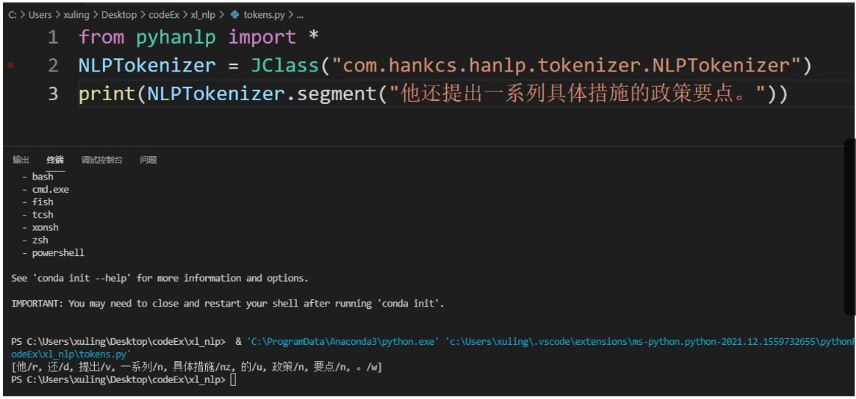
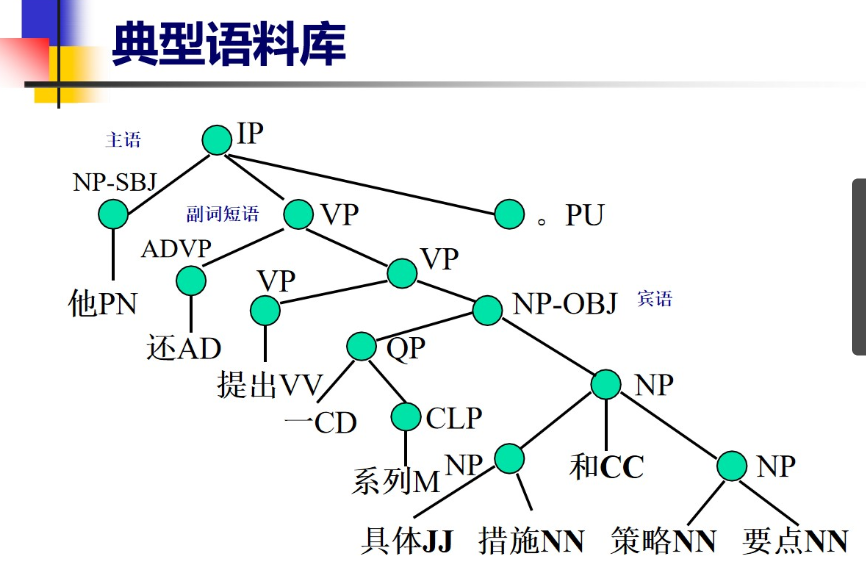

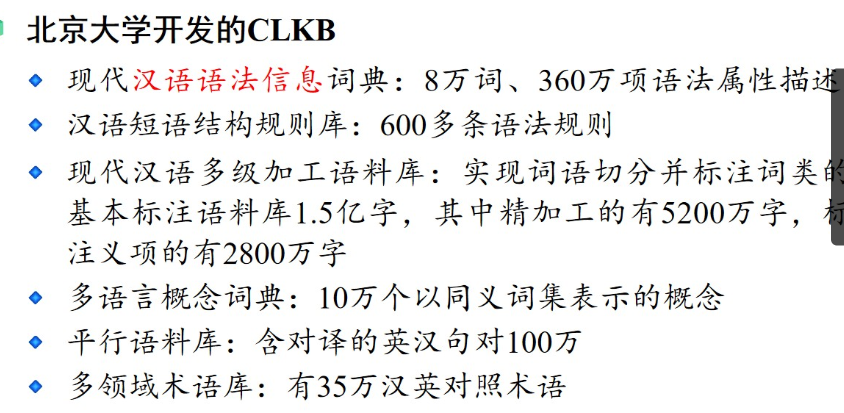

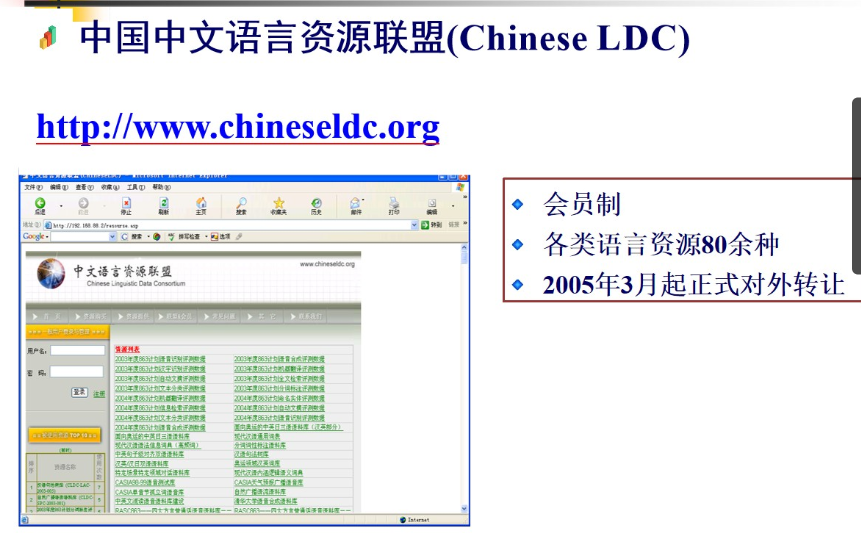

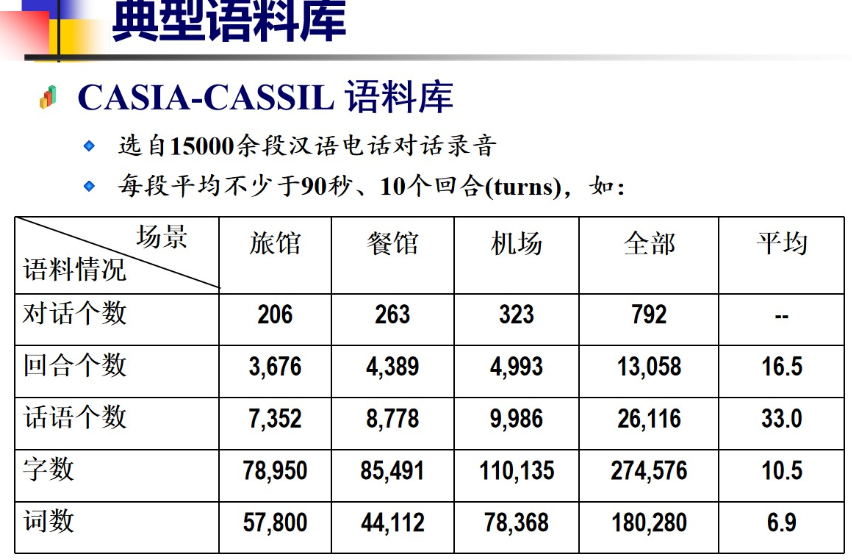
等等 过于多了
4.5 WordNet






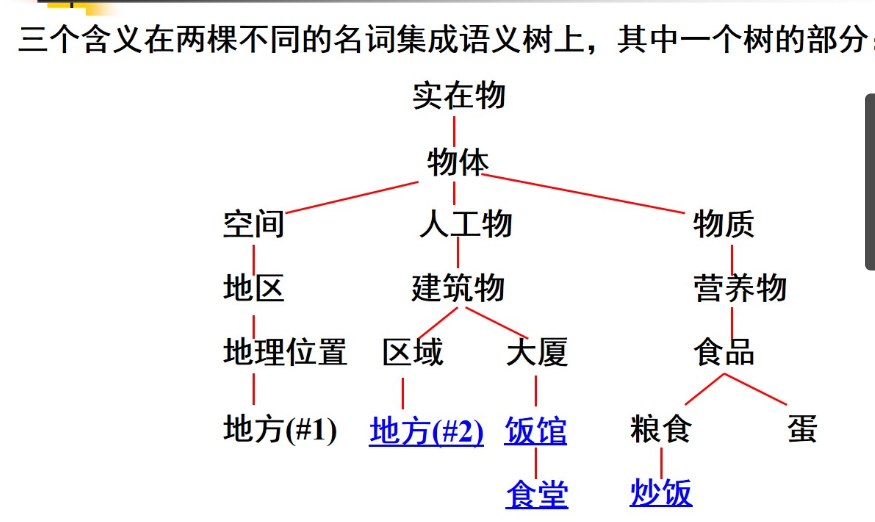
4.6 知网(HowNet)




4-1 语言模型(主要集中讲n-gram和数据平滑)


4.1基本概念


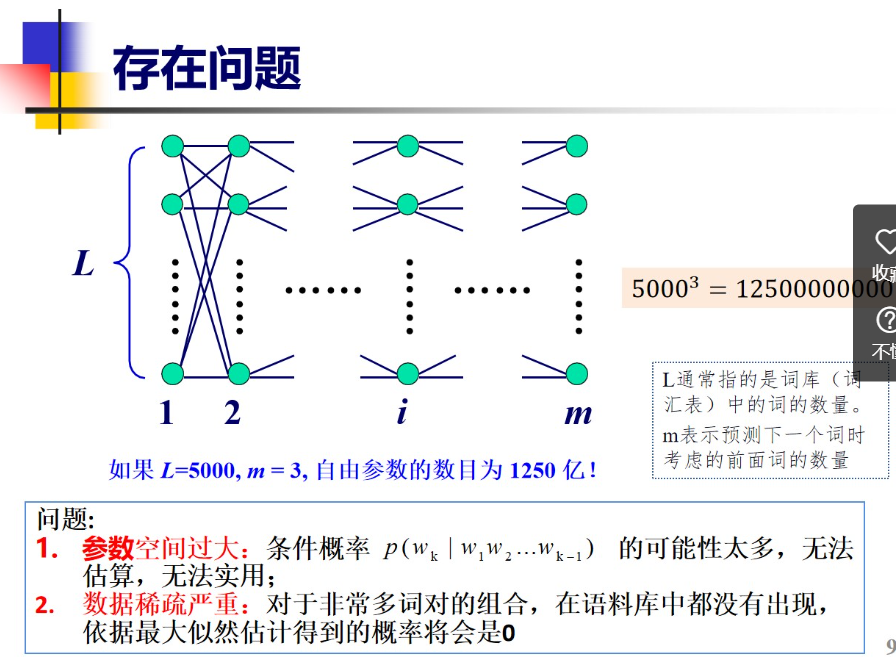

经典老模型 注意n=1,2,3
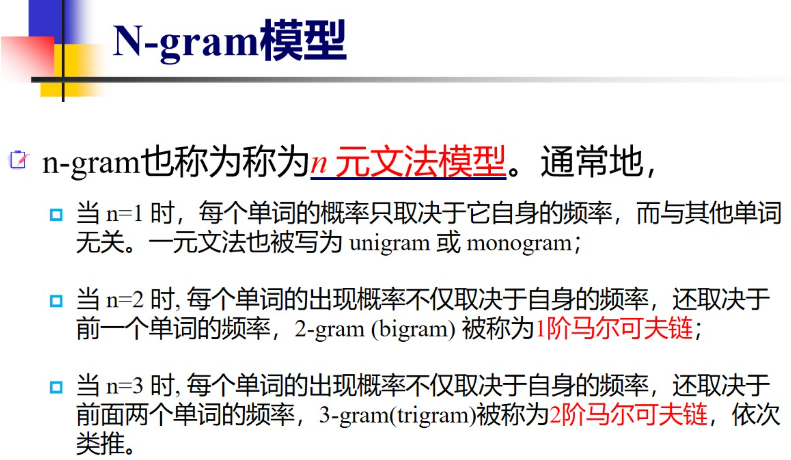


4.2参数估计(极大似然估计)

4.3数据平滑
现在存在数据稀疏问题,语料库太少了导致有些概率计算过小,出现下溢出




+1平滑 比较经典需要掌握





所有未出现n-gram相同
所有n-gram+相同频度
+delta平滑(加法平滑)

Good-Turing平滑 经典 掌握例子



案例


Katz平滑
类似优化搜索算法
进行分段 根据情况选择最优方法

线性插值平滑


lamda如何选?
可以推广 N阶往N+1阶推 思想是由低阶模型线性插值
4.4统计语言模型的评价



4.5统计语言模型的不足之处
说简单点神经网络模型更牛逼 有 自注意力机制
5 神经网络语言模型
1. 目标与背景
- 核心问题:如何用神经网络建模语言,使机器能够理解和生成自然语言?
- 出发点:从传统的统计语言模型(如 n-gram)过渡到神经网络,解决稀疏性和泛化能力不足的问题。
- 思维切入:语言是序列数据,神经网络通过学习词与词之间的关系来预测或生成文本。
2. 基本概念
- 词嵌入(Word Embedding):将单词映射为低维稠密向量,捕捉语义和句法关系(如 Word2Vec、GloVe)。
- 语言模型(Language Model):给定前文,预测下一个词的概率分布,形式化为 P(wt∣w1:t−1)P(w_t | w_{1:t-1})
P(w_t | w_{1:t-1})。- 神经网络角色:用神经网络(如 RNN、LSTM、Transformer)替代传统的计数方法,建模长期依赖和上下文。
3. 模型发展脉络
- 早期模型:基于前馈神经网络(NNLM),用固定窗口预测下一个词。
- 循环神经网络(RNN):引入序列建模能力,解决固定窗口限制,但面临梯度消失问题。
- 改进模型(LSTM/GRU):通过门控机制增强长期依赖建模能力。
- Transformer:基于自注意力机制,彻底改变语言建模方式,支持并行计算和捕捉全局上下文。
4. 关键技术与方法
- 训练目标:
- 最大似然估计:优化 logP(wt∣w1:t−1)\log P(w_t | w_{1:t-1})
\log P(w_t | w_{1:t-1})。- 自监督任务:如掩码语言模型(MLM,BERT)或因果语言模型(CLM,GPT)。
- 词嵌入学习:从独立训练(如 Skip-Gram、CBOW)到与模型联合优化(如 BERT)。
- 正则化与优化:Dropout、注意力机制、Adam 优化器等。
5. 应用与评估
- 应用场景:机器翻译、文本生成、问答系统、情感分析等。
- 评估指标:困惑度(Perplexity,衡量预测能力)、BLEU(翻译质量)、ROUGE(摘要质量)等。
- 思维重点:模型如何从输入到输出?如何衡量效果?
6. 挑战与未来
- 挑战:多义性、上下文依赖性、计算成本、跨语言泛化。
- 趋势:预训练模型(如 BERT、GPT)、多模态融合、轻量化部署。
框架总结
- 从“是什么”到“怎么做”:理解语言模型的目标 → 学习词嵌入和神经网络基础 → 掌握模型演进和技术细节 → 应用到实际任务。
- 层层递进:从静态词向量到动态上下文表示,从简单预测到复杂生成。
- 实践导向:关注输入(文本)、模型(架构)、输出(概率分布或生成结果)之间的关系。
引入 存在问题 同义词无法识别 比如 枯燥 无聊 这两个相似度机器识别为0
word embedding ??

语义空间?
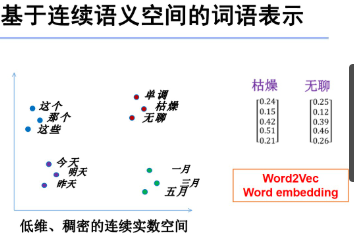
一种 word embedding的办法 Word2vec

该算法其中一种训练模式
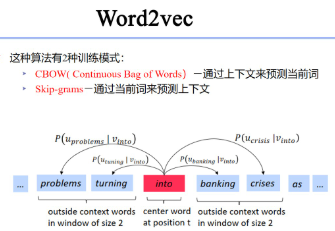

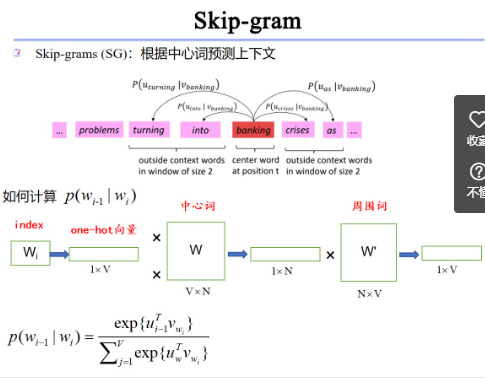
词嵌入\NNLM\Word2Vec\前馈神经网络 关系?
- 词嵌入是 NNLM 和 Word2Vec 的共同基础,作为输入表示存在。
- 前馈神经网络是 NNLM 的架构基础,Word2Vec 则对其进行了简化。
- NNLM是早期尝试,用 FNN 建模语言并生成词嵌入。
- Word2Vec是 NNLM 的优化版本,专注于高效生成词嵌入,去除了复杂的隐藏层,应用更广泛。
前馈神经网络FNN和循环神经网络RNN区别?
前馈神经网络(Feedforward Neural Network, FNN)和循环神经网络(Recurrent Neural Network, RNN)是两种常见的神经网络架构,它们在结构、功能和应用场景上有显著区别。以下是简要对比:
1. 结构差异
- 前馈神经网络 (FNN):
- 数据流是单向的:从输入层 → 隐藏层 → 输出层,没有循环或反馈。
- 层与层之间是全连接的,每一层只处理当前输入,不保留历史信息。
- 典型的静态网络,适合独立样本的处理。
- 循环神经网络 (RNN):
- 具有循环结构:隐藏层不仅接收当前输入,还接收前一时间步的隐藏状态,形成“记忆”。
- 数据流是动态的,网络在时间维度上展开,适合序列数据。
- 参数在时间步间共享。
2. 时间维度
- FNN:无时间概念,每个输入是独立的,处理时不考虑前后关系。
- RNN:引入时间维度,能够处理序列数据(如时间序列、文本),当前输出依赖于之前的输入。
3. 功能与用途
- FNN:
- 擅长静态任务,如图像分类、回归问题。
- 在 NLP 中,如 NNLM,用固定窗口处理局部上下文,无法捕捉长距离依赖。
- RNN:
- 擅长序列任务,如语言建模(预测下一个词)、机器翻译、语音识别。
- 通过“记忆”机制捕捉序列中的依赖关系。
4. 计算方式
- FNN:
- 计算简单,前向传播一次性完成。
- 输出 y=f(Wx+b)y = f(Wx + b)
y = f(Wx + b),其中 xxx是输入,WWW和 bbb是权重和偏置。- RNN:
- 计算复杂,前向传播随时间步递推。
- 隐藏状态 ht=f(Wxhxt+Whhht−1+b)h_t = f(W_{xh}x_t + W_{hh}h_{t-1} + b)
h_t = f(W_{xh}x_t + W_{hh}h_{t-1} + b),其中 ht−1h_{t-1}h_{t-1}是前一状态。5. 优缺点
- FNN:
- 优点:结构简单,计算效率高,易于并行化。
- 缺点:无法处理序列数据,缺乏记忆能力。
- RNN:
- 优点:能建模时间依赖关系,适合动态数据。
- 缺点:梯度消失/爆炸问题,难以捕捉长期依赖(改进版如 LSTM/GRU 解决)。
6. NLP 中的应用对比
- FNN:如 NNLM,用固定窗口预测下一个词,上下文范围有限。
- RNN:如基于 RNN 的语言模型,能处理变长序列,捕捉更广的上下文。
神经网络语言模型学习框架?思路?
简明总结
- 本质:神经网络语言模型是用神经网络建模语言概率。
- 演进:FNN → RNN → LSTM → Transformer。
- 学习路径:基础概念 → 模型结构 → 实践应用 → 优化扩展。
1. 核心概念
- 什么是神经网络语言模型?
- 用神经网络预测语言序列的概率分布,如 P(wt∣w1:t−1)P(w_t | w_{1:t-1})
P(w_t | w_{1:t-1}),即给定前文预测下一个词。 - 目标:取代传统统计模型(如 n-gram),解决稀疏性和泛化问题。
- 用神经网络预测语言序列的概率分布,如 P(wt∣w1:t−1)P(w_t | w_{1:t-1})
- 关键要素:
- 词嵌入:将单词转化为向量,作为模型输入。
- 神经网络:建模词间关系,捕捉上下文依赖。
- 输出:概率分布或生成文本。
2. 发展脉络
- 前馈神经网络语言模型 (NNLM):
- 提出者:Bengio (2003)。
- 结构:输入层(词嵌入)→ 隐藏层 → 输出层。
- 特点:固定窗口,学习词嵌入,计算复杂。
- 循环神经网络语言模型 (RNN-LM):
- 提出者:Mikolov (2010)。
- 结构:引入循环,隐藏状态随时间步更新。
- 特点:处理变长序列,建模长期依赖。
- 改进模型 (LSTM/GRU):
- 解决:RNN 的梯度消失问题。
- 特点:门控机制,增强长距离依赖捕捉。
- Transformer 模型:
- 提出者:Vaswani (2017)。
- 结构:自注意力机制,无循环,支持并行。
- 特点:全局上下文建模,主导现代 NLP(如 BERT、GPT)。
3. 技术细节
- 输入表示:
- 词嵌入:静态(如 Word2Vec)→ 动态(如 BERT)。
- 处理:分词、字符嵌入、子词单元(如 BPE)。
- 训练目标:
- 最大化似然:$logP(wt∣w1:t−1)\log P(w_t | w_{1:t-1})
\log P(w_t | w_{1:t-1})$。 - 自监督:掩码预测(MLM)、因果预测(CLM)。
- 最大化似然:$logP(wt∣w1:t−1)\log P(w_t | w_{1:t-1})
- 优化方法:
- 损失函数:交叉熵。
- 技术:负采样、层次 Softmax、Adam 优化。
- 评估指标:
- 困惑度(Perplexity):衡量预测能力。
- 下游任务:BLEU、F1 等。
4. 应用场景
- 文本生成:聊天机器人、文章续写。
- 机器翻译:序列到序列建模。
- 问答系统:上下文理解。
- 情感分析:序列分类。
5. 挑战与趋势
- 挑战:
- 长距离依赖:早期模型不足,Transformer 解决。
- 计算成本:大规模预训练资源需求高。
- 多语言泛化:跨语言适配问题。
- 趋势:
- 预训练 + 微调:如 BERT、GPT。
- 多模态融合:文本 + 图像/语音。
- 轻量化:DistilBERT、MobileBERT。
总结:完整的NLP学习框架
- N-Gram
- 学习基础统计模型,理解其简单性和局限性。
- 前馈神经网络(NNLM)
- 引入神经网络和词嵌入,掌握语义表示。
- Word2Vec(CBOW与Skip-gram)
- 深入词嵌入的高效生成与应用。
- 循环神经网络(RNN)
- 理解序列建模及其挑战。
- LSTM与GRU
- 解决长依赖问题,提升序列处理能力。
- Transformer
- 掌握自注意力与现代NLP的核心技术。
Transformer很重要
包含编码器和解码器两个重要组件 以及自注意力机制这个重要插件
6 隐马尔可夫模型
前向算法? 动态规划思想
例题 必考


好的,我现在需要根据用户提供的图片信息,猜测这幅图的题目,并给出它的计算过程。用户已经告诉我图片的题目是“前向算法求解实例”,不过可能他们希望我验证这个猜测是否正确,并详细解释计算过程。首先,我需要仔细分析用户提供的图片描述,理解其中的各个部分,然后按照前向算法的步骤来解析每个时间步的计算。
首先,确认题目是否正确。根据用户描述,图片的标题确实是“前向算法求解实例”,所以这个猜测是正确的。接下来需要详细解释前向算法在这里的应用过程。
图片中的关键元素包括隐藏状态集合Q={盒子1,盒子2,盒子3},观测状态集合V={红,白},观测序列O={红,白,红}。还有初始概率π,状态转移矩阵A,观测概率矩阵B。接下来分三个时间步t=1,2,3计算前向概率,最后得到观测序列的概率P(O|λ)=0.13022。
首先,我需要回顾前向算法的基本步骤。前向算法用于计算给定HMM模型λ下观测序列O的概率。它通过递推计算前向概率α_t(i),表示在时间t处于状态i且观测到前t个观测值的概率。具体步骤包括初始化、递推和终止。
根据用户提供的图片中的详细文本,比如初始概率π=(0.2,0.4,0.4)^T,状态转移矩阵A和观测概率矩阵B的具体数值,我需要将这些数值代入公式,分步计算每个时间点的α值。
首先处理t=1的情况。初始时刻,观测到第一个红色球。计算每个隐藏状态的α1(i)=π_i * b_i(o1)。例如,α1(1)=0.20.5=0.1,α1(2)=0.40.4=0.16,α1(3)=0.4*0.7=0.28。然后这三个值加起来就是当前的前向概率,不过可能在t=1时暂时不需要求和,而是保存每个状态的α值用于下一步。
接下来是t=2,观测到白色球。此时需要计算每个隐藏状态的α2(j)=Σ{i=1}^3 α1(i)*a{ij} * b_j(o2)。例如,计算α2(1)=α1(1)a_{11}b1(白) + α1(2)a_{21}b1(白) + α1(3)a_{31}b1(白)。根据用户提供的图片中的数值,可能a_{11}=0.5(从盒子1转移到盒子1的概率),a_{21}=0.3(从盒子2转移到盒子1的概率),a_{31}=0.2(从盒子3转移到盒子1的概率)。而b1(白)是盒子1生成白色球的概率,根据用户提供的B矩阵,可能盒子1生成白色的概率是0.5?这里需要确认。用户提到B矩阵中,盒1的观测概率是0.5和0.5?例如,盒1生成红球是0.5,白球也是0.5?或者可能用户描述中有不同的数值?
根据用户给出的文本中有:
B=盒2 0.4 0.6,盒3 0.7 0.3。可能盒1的观测概率是红0.5,白0.5,盒2是红0.4,白0.6,盒3是红0.7,白0.3?但用户提到的观测序列第一个是红色,所以在t=1时,b_i(o1)是红对应的概率。例如,盒1生成红的概率是0.5,盒2是0.4,盒3是0.7。然后在t=2时,观测到白色,所以此时b_j(o2)是白的概率:盒1的0.5,盒2的0.6,盒3的0.3?
可能用户提供的图片中的B矩阵如下:
对于观测红和白,各隐藏态的发射概率:
盒1: 红0.5,白0.5;
盒2: 红0.4,白0.6;
盒3: 红0.7,白0.3?
或者可能相反?比如盒3的红概率是0.7,那么白是0.3。而盒2的红是0.4,白0.6。盒1的红0.5,白0.5。这样在t=1观测红时,各状态的b_i(红)是0.5, 0.4, 0.7。然后t=2观测白时,b_i(白)是0.5, 0.6, 0.3。这样计算。
接下来计算α2(1)的时候,需要把t=1的α1(i)乘以对应的转移概率a_ij,再乘以b_j(o2)。例如,计算α2(1) = α1(1)a_11b1(白) + α1(2)a_21b1(白) + α1(3)a_31b1(白)。代入数值:0.10.50.5(对吗?)或者可能状态转移的矩阵是行表示当前状态,列表示下一状态?比如A矩阵的行是当前状态i,列是下一状态j。例如,A矩阵的结构:
A = [
[0.5, 0.2, 0.3], // 从盒1转移到盒1、盒2、盒3的概率
[0.3, 0.5, 0.2], // 盒2的转移概率
[0.2, 0.3, 0.5] // 盒3的转移概率
]
这样,a_{ij}是从状态i转移到状态j的概率。比如从盒1到盒2的概率是0.2。
所以,在计算α2(j)时,对于每个j,需要累加所有i的α1(i)*a_{i,j},然后乘以b_j(o2)。
例如,计算α2(1):
= (α1(1)a_{1,1} + α1(2)a_{2,1} + α1(3)*a_{3,1}) ) * b_1(白)
根据用户给出的数据,可能用户在t=2时的计算示例中有:
α2(1) = [0.10.5 + 0.160.3 + 0.28*0.2] * b1(白)。这里,用户给出的文本中有一段:
α2(1)=[α11b1(a21i]b1(a21iobl2(a11jbl02)=[0.10.5+0.160.3+0.28*0.2] * b1(白)。假设这里的计算是α2(1) = (0.10.5 + 0.160.3 + 0.28*0.2) * b1(白)。这里的a_{i,j}分别是盒1到盒1的0.5,盒2到盒1的0.3,盒3到盒1的0.2。然后乘以b1(白)=0.5。这样计算的话:
0.1*0.5 = 0.05;
0.16*0.3=0.048;
0.28*0.2=0.056;
总和是0.05+0.048+0.056=0.154;
然后乘以b1(白)=0.5,得到α2(1)=0.154*0.5=0.077?
但根据用户给出的文本中,α2(1)的计算可能写得更复杂,比如用户提供的文本中有:
α2(1)=[α11b1(a21i]b1(a21iobl2(a11jbl02)=[0.10.5+0.160.3+0.28*0.2] * … 这里的表达式可能有误,但数值部分是正确的。例如,用户可能想表达α2(1) = [0.10.5 + 0.160.3 + 0.28*0.2] * b1(白)。假设这里的b1(白)是0.5,所以得到0.154*0.5=0.077。但根据用户提供的后续结果,比如t=2时的α2(1)、α2(2)、α2(3)的值可能不同,需要看最终的数值结果。
根据用户给出的最终结果,P(O|λ)=0.13022,是三个时间步后的总和。现在需要逐步计算每个时间步的值,并确保中间的步骤正确。
现在,我需要按照标准前向算法的步骤,结合用户提供的数据,重新计算各个α的值,并确保结果与图片中的一致。这可能包括:
- 初始化:计算α1(i) = π_i * b_i(o1),对于每个i∈{1,2,3}。
- 对于t=2到T:
αt(j) = [Σ{i=1}^N α{t-1}(i) * a{i,j}] * b_j(o_t) - 终止:P(O|λ) = Σ_{i=1}^N α_T(i)
现在,用户提供的图片中给出了三个时间步的计算,每个时间步的α值:
t=1时:
α1(1)=0.1;
α1(2)=0.16;
α1(3)=0.28;
t=2时,计算白色球的概率:
例如,α2(1)的计算方式如上,得到0.077?或者根据用户给出的文本中,可能实际计算的值是:
用户提到:“α2(1)=[α11b1(a21i]b1(a21iobl2(a11jbl02)=[0.10.5+0.160.3+0.28*0.2] * …”,假设后面的乘数是b_j(o2)即白色球的概率。例如,盒1的白色概率是0.5,所以乘0.5:
[0.10.5(这是a_{1,1}) + 0.160.3(a_{2,1}) + 0.280.2(a_{3,1}) ] = 0.05 + 0.048 + 0.056 = 0.154。然后乘以b1(白)=0.5,得到α2(1)=0.1540.5=0.077。
同样的,计算α2(2):
= [α1(1)a_{1,2} + α1(2)a_{2,2} + α1(3)*a_{3,2}] * b2(白)
其中,a_{1,2}=0.2,a_{2,2}=0.5,a_{3,2}=0.3。所以,
0.1*0.2=0.02;
0.16*0.5=0.08;
0.28*0.3=0.084;
总和是0.02+0.08+0.084=0.184;
乘以b2(白)=0.6(盒2的白色概率),得到0.184*0.6=0.1104。这可能对应用户提到的α2(2)=0.1104。
然后计算α2(3):
= [α1(1)a_{1,3} + α1(2)a_{2,3} + α1(3)*a_{3,3}] * b3(白)
a_{1,3}=0.3,a_{2,3}=0.2,a_{3,3}=0.5;
计算:
0.1*0.3=0.03;
0.16*0.2=0.032;
0.28*0.5=0.14;
总和0.03+0.032+0.14=0.202;
乘以b3(白)=0.3,得到0.202*0.3=0.0606。所以α2(3)=0.0606。
这样,t=2时的三个α值为0.077,0.1104,0.0606。
接下来是t=3,观测到红色球。此时,需要计算α3(1)、α3(2)、α3(3)。
例如,计算α3(1):
= [α2(1)a_{1,1} + α2(2)a_{2,1} + α2(3)*a_{3,1}] * b1(红)
这里,a_{1,1}=0.5,a_{2,1}=0.3,a_{3,1}=0.2;
计算:
0.077*0.5=0.0385;
0.1104*0.3=0.03312;
0.0606*0.2=0.01212;
总和0.0385+0.03312+0.01212=0.08374;
乘以b1(红)=0.5,得到α3(1)=0.08374*0.5=0.04187,与用户给出的α3(1)=0.04187一致。
同样,计算α3(2):
= [α2(1)a_{1,2} + α2(2)a_{2,2} + α2(3)*a_{3,2}] * b2(红)
a_{1,2}=0.2,a_{2,2}=0.5,a_{3,2}=0.3;
计算:
0.077*0.2=0.0154;
0.1104*0.5=0.0552;
0.0606*0.3=0.01818;
总和0.0154+0.0552+0.01818=0.08878;
乘以b2(红)=0.4,得到0.08878*0.4=0.035512,四舍五入为0.03551,与用户给出的α3(2)=0.03551一致。
最后,计算α3(3):
= [α2(1)a_{1,3} + α2(2)a_{2,3} + α2(3)*a_{3,3}] * b3(红)
a_{1,3}=0.3,a_{2,3}=0.2,a_{3,3}=0.5;
计算:
0.077*0.3=0.0231;
0.1104*0.2=0.02208;
0.0606*0.5=0.0303;
总和0.0231+0.02208+0.0303=0.07548;
乘以b3(红)=0.7,得到0.07548*0.7=0.052836,四舍五入为0.05284,与用户给出的α3(3)=0.05284一致。
最后,P(O|λ)=α3(1)+α3(2)+α3(3)=0.04187+0.03551+0.05284≈0.13022,与用户给出的结果一致。
综上所述,计算过程正确,每个时间步都按照前向算法的递推公式计算,并最终得到了正确的观测序列概率。
这幅图的题目是“前向算法求解实例”,展示了如何通过隐马尔可夫模型(HMM)的前向算法计算观测序列的概率。以下是详细的计算过程:
模型参数
- 隐藏状态集合:( Q = {\text{盒子1}, \text{盒子2}, \text{盒子3}} ),共3个状态。
- 观测状态集合:( V = {\text{红}, \text{白}} ),共2个观测状态。
- 观测序列:( O = {\text{红}, \text{白}, \text{红}} )。
- 初始概率:( \pi = (0.2, 0.4, 0.4)^T )。
- 状态转移矩阵 ( A ):
[
A = \begin{bmatrix}
0.5 & 0.2 & 0.3 \
0.3 & 0.5 & 0.2 \
0.2 & 0.3 & 0.5
\end{bmatrix}
] - 观测概率矩阵 ( B ):
[
B = \begin{cases}
\text{盒子1}: \text{红}=0.5, \text{白}=0.5 \
\text{盒子2}: \text{红}=0.4, \text{白}=0.6 \
\text{盒子3}: \text{红}=0.7, \text{白}=0.3
\end{cases}
]
前向算法计算过程
前向算法通过递推计算前向概率 ( \alpha_t(i) ),表示在时间 ( t ) 处于状态 ( i ) 并观测到前 ( t ) 个观测值的概率。
1. 初始化(t=1)
计算第一个观测 ( O_1 = \text{红} ) 的前向概率:
[
\alpha_1(i) = \pi_i \cdot b_i(O_1)
]
- ( \alpha_1(1) = 0.2 \times 0.5 = 0.1 )
- ( \alpha_1(2) = 0.4 \times 0.4 = 0.16 )
- ( \alpha_1(3) = 0.4 \times 0.7 = 0.28 )
2. 递推(t=2)
计算第二个观测 ( O_2 = \text{白} ) 的前向概率:
[
\alpha_2(j) = \left[ \sum_{i=1}^3 \alpha_1(i) \cdot a_{ij} \right] \cdot b_j(O_2)
]
- 盒子1:
[
\alpha_2(1) = (0.1 \times 0.5 + 0.16 \times 0.3 + 0.28 \times 0.2) \times 0.5 = 0.077
] - 盒子2:
[
\alpha_2(2) = (0.1 \times 0.2 + 0.16 \times 0.5 + 0.28 \times 0.3) \times 0.6 = 0.1104
] - 盒子3:
[
\alpha_2(3) = (0.1 \times 0.3 + 0.16 \times 0.2 + 0.28 \times 0.5) \times 0.3 = 0.0606
]
3. 递推(t=3)
计算第三个观测 ( O_3 = \text{红} ) 的前向概率:
[
\alpha_3(j) = \left[ \sum_{i=1}^3 \alpha_2(i) \cdot a_{ij} \right] \cdot b_j(O_3)
]
- 盒子1:
[
\alpha_3(1) = (0.077 \times 0.5 + 0.1104 \times 0.3 + 0.0606 \times 0.2) \times 0.5 = 0.04187
] - 盒子2:
[
\alpha_3(2) = (0.077 \times 0.2 + 0.1104 \times 0.5 + 0.0606 \times 0.3) \times 0.4 = 0.03551
] - 盒子3:
[
\alpha_3(3) = (0.077 \times 0.3 + 0.1104 \times 0.2 + 0.0606 \times 0.5) \times 0.7 = 0.05284
]
4. 终止
观测序列概率为所有终态前向概率之和:
[
P(O|\lambda) = \sum_{i=1}^3 \alpha_3(i) = 0.04187 + 0.03551 + 0.05284 = 0.13022
]
最终结果
观测序列 ( O = {\text{红}, \text{白}, \text{红}} ) 的概率为 0.13022。图中通过表格和公式清晰展示了每一步的计算过程。
Viterbi 搜索算法