converge corroborate credulous cynical dearth decipher decorum deduce deference defiant delineate denounce deplete deprecate deride diligent discern disdain disparate dispel
commence panorama audacious bolster augment candid concede complacent capricious concise censure coherent cogent condone astute 单词词根分解含义记忆联想commencecom- (一起) + mence (开始)开始"Come on, let's start!"panoramapan- (全部) + orama (景象)全景"Pan of the drama" (整个视野)audaciousaud- (勇敢) + -acious (形容词)大胆的"Odd and da…
Review Contempt蔑视 Captive非自愿 Huddle
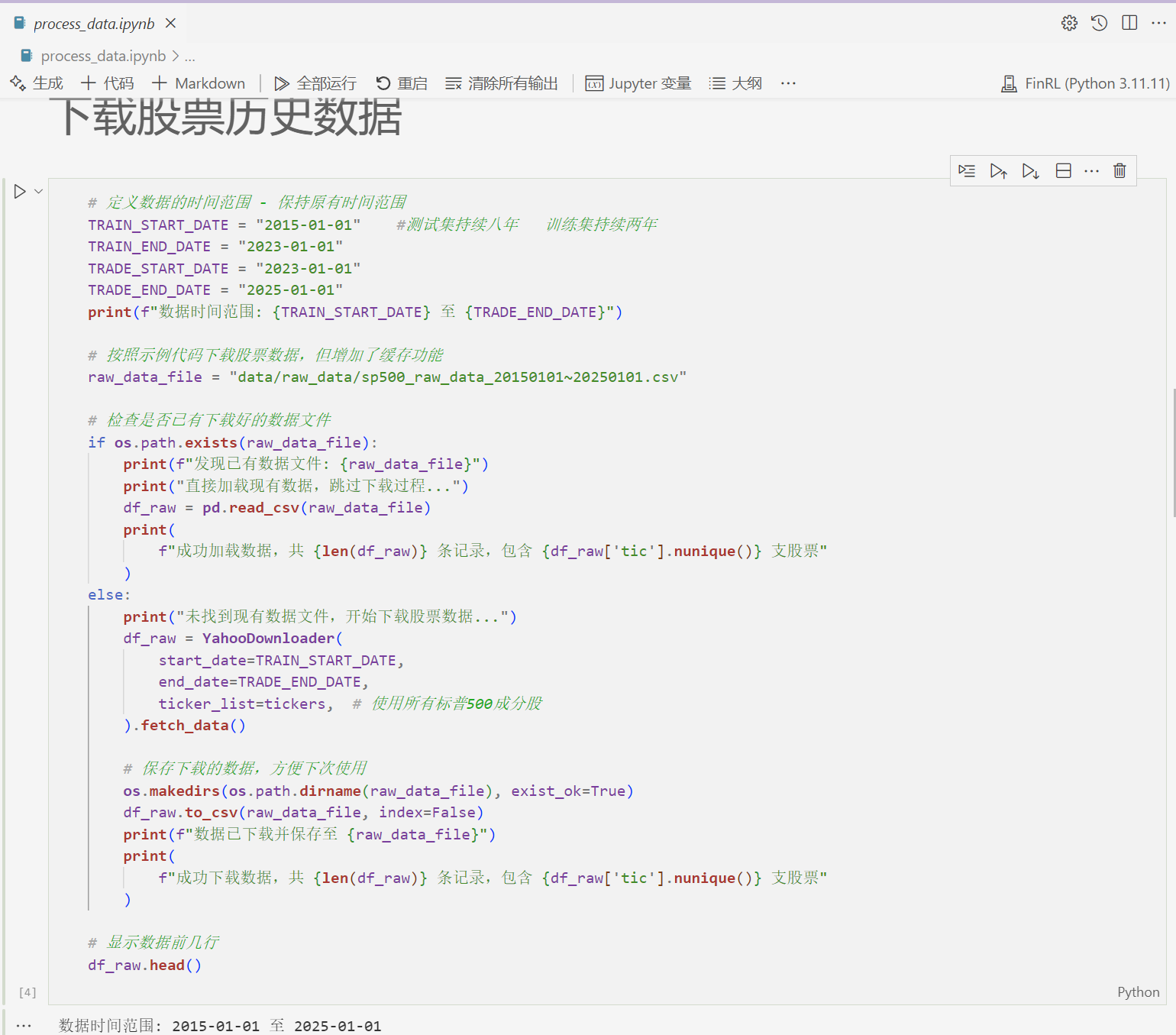
使用 Superset 处理股票数据并进行可视化分析Superset+Echarts
密码保护:FinRL 学习与开发
金融术语

1. 引言 目的:探讨如何使用 Superset 处理股票数据并进行可视化分析。 背景:提及之前相关博客,提供背景和上下文。 相关文章:《Anscombe 数据集的可视化与回归分析:Superset、Metabase 和 Redash 的应用与对比》 2. 为什么选择 Superset 和 ECharts 2.1 选择 Superset 的理由 优势: 开源且功能强大,支持多种数据源。 提供灵活的仪表盘和图表定制能力。 不重新开发 BI 工具的原因: 开发成本高,时间长。 Superset 已成熟,社区支持广泛。 2.2 选择 ECharts 的理由 特点: 轻量且高效,支持丰富的图表类型。 …
这篇文章受密码保护,输入密码才能阅读
基本面 市盈率(PE)Price-to-Earning Ratio 定义:市盈率是股价与每股收益(EPS)的比率,或公司市值与净利润的比值,反映投资者为每单位盈利支付的价格。公式: 静态市盈率 = 当前股价 ÷ 上年度每股收益 动态市盈率 = 当前股价 ÷ 预测本年度每股收益举例:若某股票当前价格20元,去年每股收益4元,则静态市盈率为5倍(即20÷4)。若预测今年每股收益增长至5元,则动态市盈率为4倍(即20÷5)5。 适用场景: 适合盈利稳定、周期性弱的行业(如消费、公用事业)45; 通过历史分位数或同行业对比判断估值高低45。局限性:无法评估亏损企业或高成长公司…
NLP学习笔记
2025/3/7 CET6
如何查看网站用的什么服务器?如何导出备份数据库?
如何翻译”巅峰产生虚伪的拥护,黄昏见证真正的使徒”
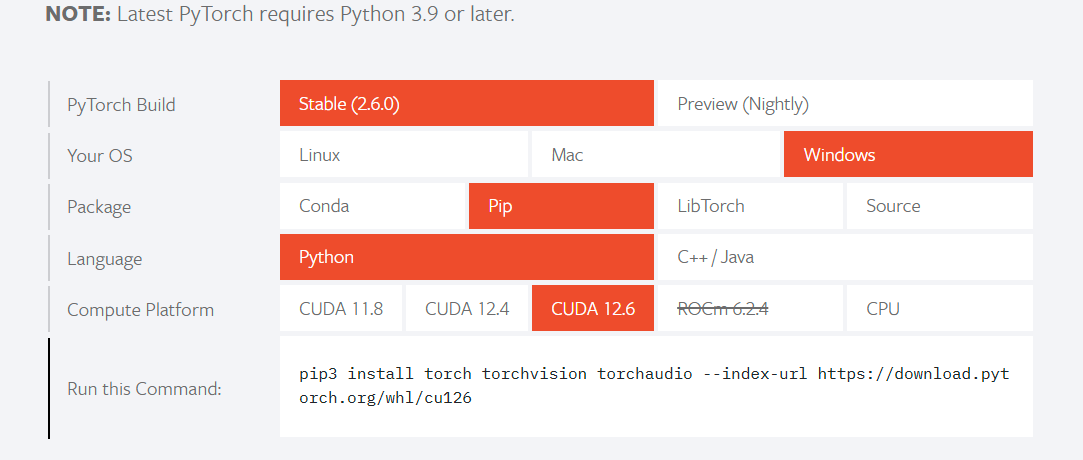
前置知识 pypi 清华镜像源使用 网址:https://mirrors.tuna.tsinghua.edu.cn/help/pypi/ 临时使用:pip install -i https://mirrors.tuna.tsinghua.edu.cn/pypi/web/simple some-package 将镜像源设为默认: # 先升级pip, 然后进行配置 python -m pip install --upgrade pip pip config set global.index-url https://mirrors.tuna.tsinghua.edu.cn/pypi/web/simp…
decree inflict sth(like harm or damage) on ... =make them suffer it indulge in sth 沉迷于 Be immersed in Be addicted to 含义:强调上瘾、无法自拔,带有较强的负面意味。 例句:He’s addicted to gambling.(他沉迷于赌博。) 与“indulge in”的区别:更强调依赖性,语气更重。 Be immersed in 含义:完全沉浸于某事物,偏中性,可用于积极或消极语境。 例句:She’s immersed in her studies.(她沉浸于学习中。) 与“i…
ubuntu22 查看WordPress网站数据库类型并导出数据库 查看WordPress使用的数据库类型 WordPress大多数情况下使用MySQL或MariaDB数据库,很少使用PostgreSQL。以下是在Ubuntu 22上确定数据库类型的方法: 方法1:查看WordPress配置文件 # 找到WordPress安装目录,查看wp-config.php文件 cd /var/www/html/你的网站目录 # 调整为你的WordPress安装路径 cat wp-config.php | grep …
地道版本: "At the peak, false followers emerge; at dusk, true apostles are revealed." “巅峰产生虚伪的拥护” “巅峰”:用 "peak" 表示,象征高潮或顶点。 “虚伪的拥护”:翻译为 "false followers",既简洁又传达了“虚伪的支持者”之意,符合英语中对伪善者的常见描述。 “黄昏见证真正的使徒” “黄昏”:用 "dusk" 表示,比 "evening" 更具诗意和象征意义,与“巅峰”形成对比。 “真正的使徒”:翻译为 "true apostles","apostles" 有“使徒、忠实追随者”的含义,…