1.

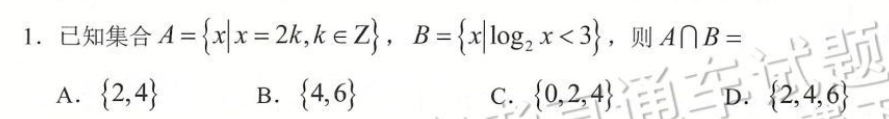
D

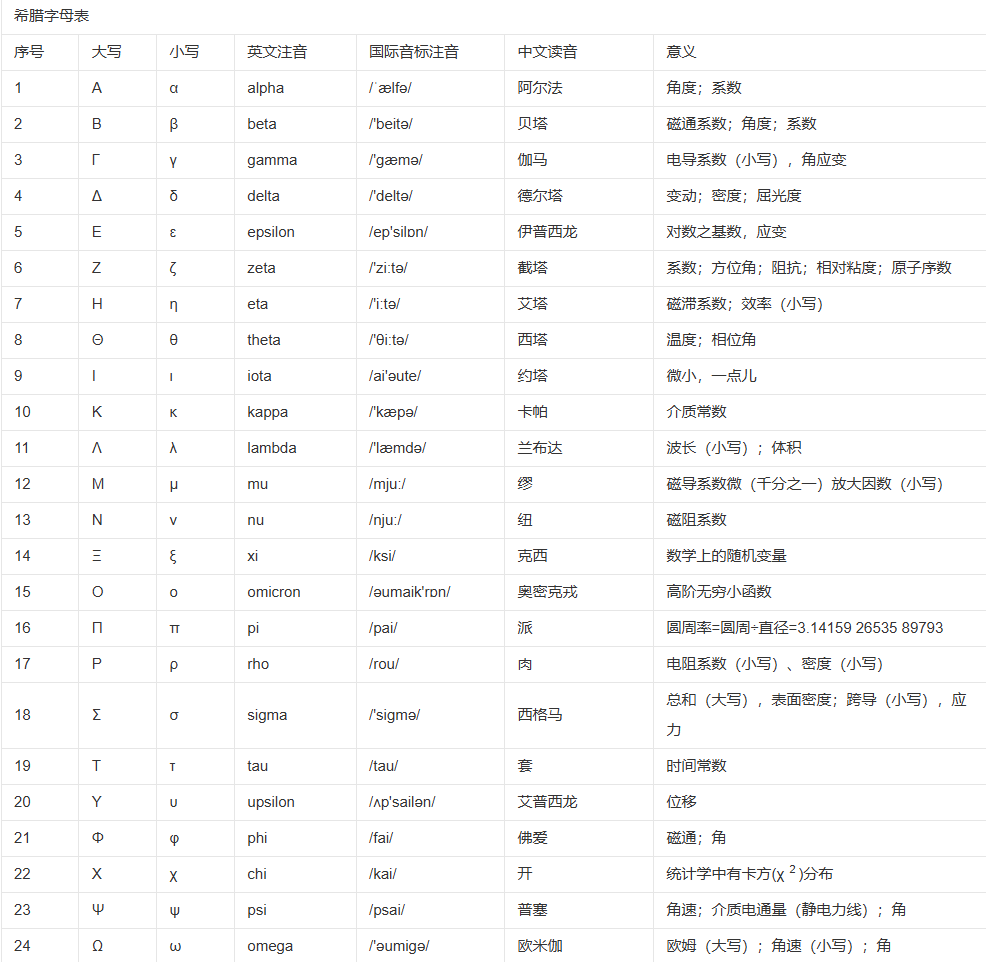
1.1集合相关的一些符号

Z整数，

N自然数

N+ N*

Q有理数

1.11111…..不包括无限不循环小数 3.14159…(为何呢? 因为所有无限循环小数 可以转换成分数 方法:令数据为x 构造消去循环部分)

R 实数 (不包括i虚数)

包括无限不循环小数 pi

属于∈

子集符号 可以取等

真子集 区别 不能取等

空集的概念

1.2 对数相关概念

为了解决指数

众所周知2^{2}=4,那么2^{x}=3?

x=log_2{3} 2是底数 3是真数

x=log_{a}b 

a^x =b a∈(0,1)∪(1,+∞)

b∈(0,+∞)

(-2)^{2} =4

研究对数的目的? 从哪引入对数的

研究指数的时候引入的

学过指数函数 y=a^x (a大于0且不等于1)

幂函数 y=x^{b} x为底数 b为幂

指数函数y=a^x x为指数

对数函数 y=logax x为真数

图像有点意思

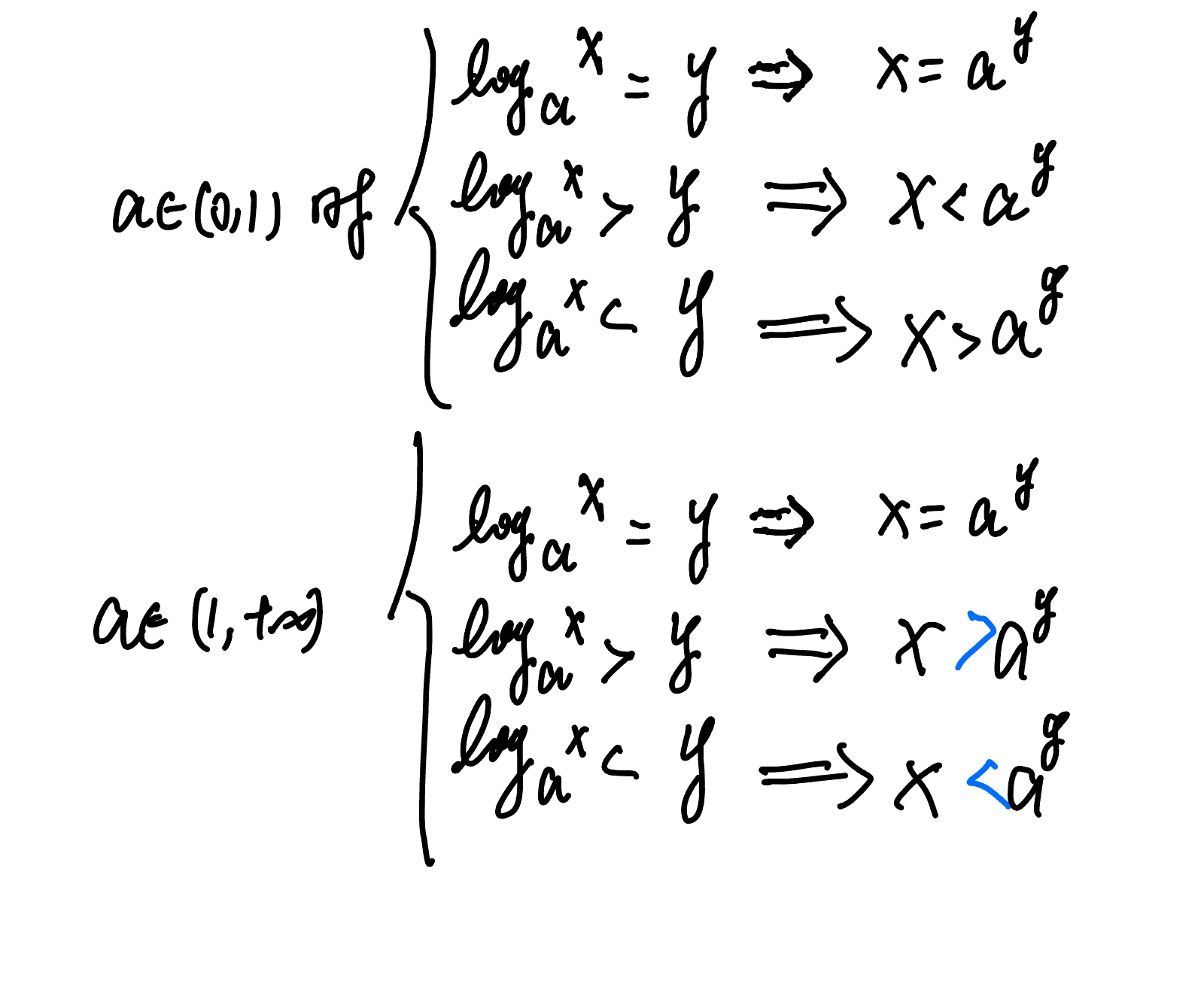
1.3 交并补

以下是集合论中交（Intersection）、并（Union）和补（Complement）的简要笔记：

1. 交（Intersection）:
   • 记号：∩
   • 定义：两个或多个集合的交集是指同时属于这些集合的所有元素组成的集合。
   • 例子：如果 A = {1, 2, 3} 和 B = {2, 3, 4}，那么 A ∩ B = {2, 3}。
2. 并（Union）:
   • 记号：∪
   • 定义：两个或多个集合的并集是指属于这些集合中的至少一个的所有元素组成的集合。
   • 例子：如果 A = {1, 2, 3} 和 B = {2, 3, 4}，那么 A ∪ B = {1, 2, 3, 4}。
3. 补（Complement）:
   • 记号：’ (一个直角 非)或 C
   • 定义：集合A的补集是指在一个给定的全集U中，不属于A的所有元素组成的集合。
   • 例子：如果 U = {1, 2, 3, 4, 5} 和 A = {1, 2, 3}，那么 A’ 或 AC = {4, 5}。

以下是交并补的基本性质：

• 交换律：A ∩ B = B ∩ A，A ∪ B = B ∪ A
• 结合律：A ∩ (B ∩ C) = (A ∩ B) ∩ C，A ∪ (B ∪ C) = (A ∪ B) ∪ C
• 分配律：A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)，A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
• 德摩根定律：(A ∪ B)’ = A’ ∩ B’，(A ∩ B)’ = A’ ∪ B’ (注意这个符号是非)
• 补集的补集：(A’)’ = A

这些笔记提供了交并补的基本概念和性质，是集合论中的基础知识点。

2

D

2.1 复数

3

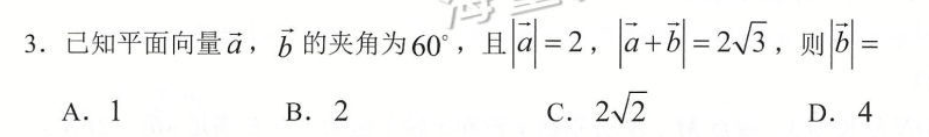
3.1 解三角形做法几何做法

正弦定理

3.2 向量解法代数做法

～遇模平方注意点乘COS 投影

4

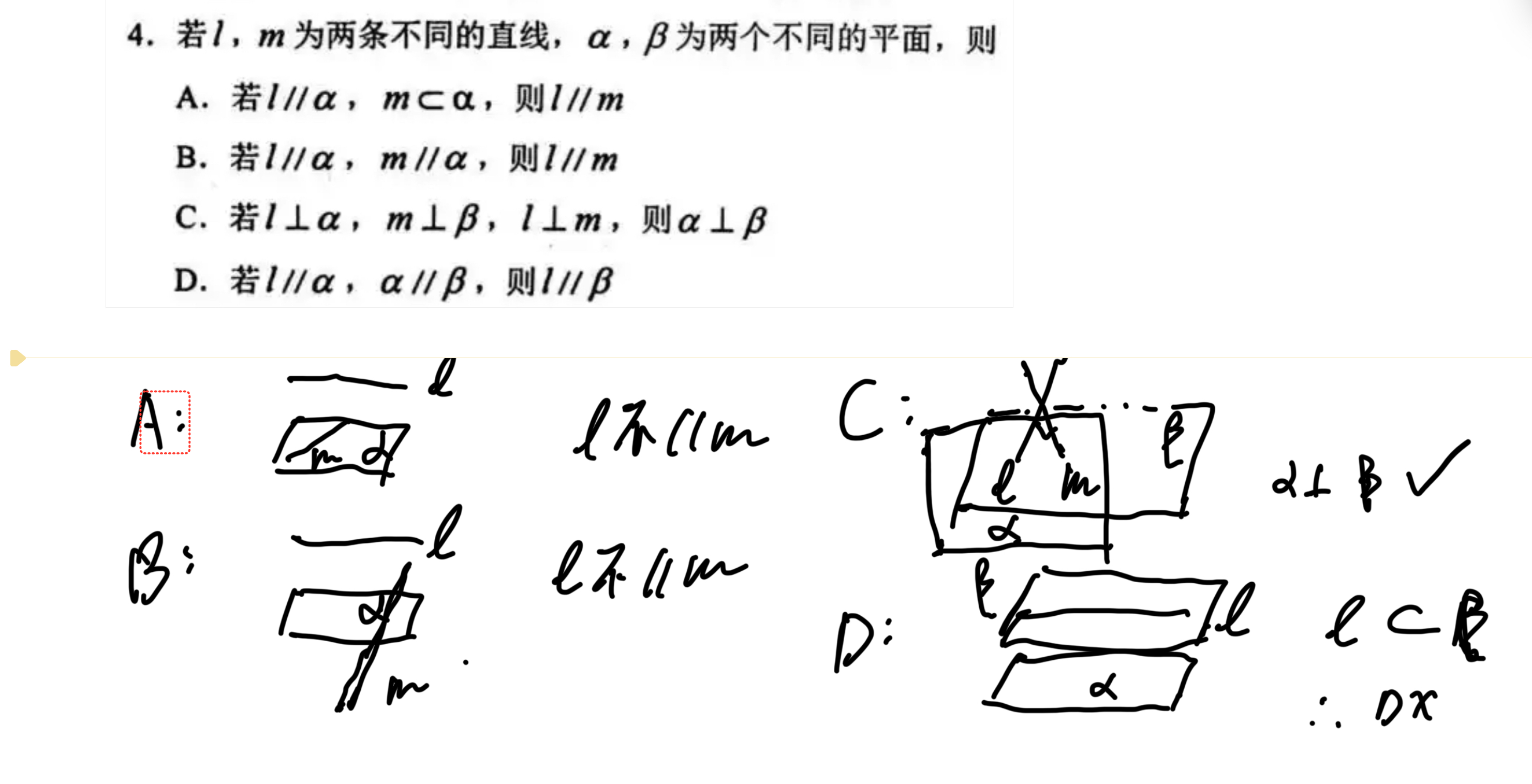
考立体几何 线面平行垂直关系

本题重点在 若直线属于平面 不平行

5

5.1方差的概念

离谱

瞪眼法 看出来 直观感受方差是波动幅度 震荡幅度

x1=1 x2=2.3 x3=3.8 x4=9 x5=4 x6=6.2

6

6.1扇形公式

推导过程

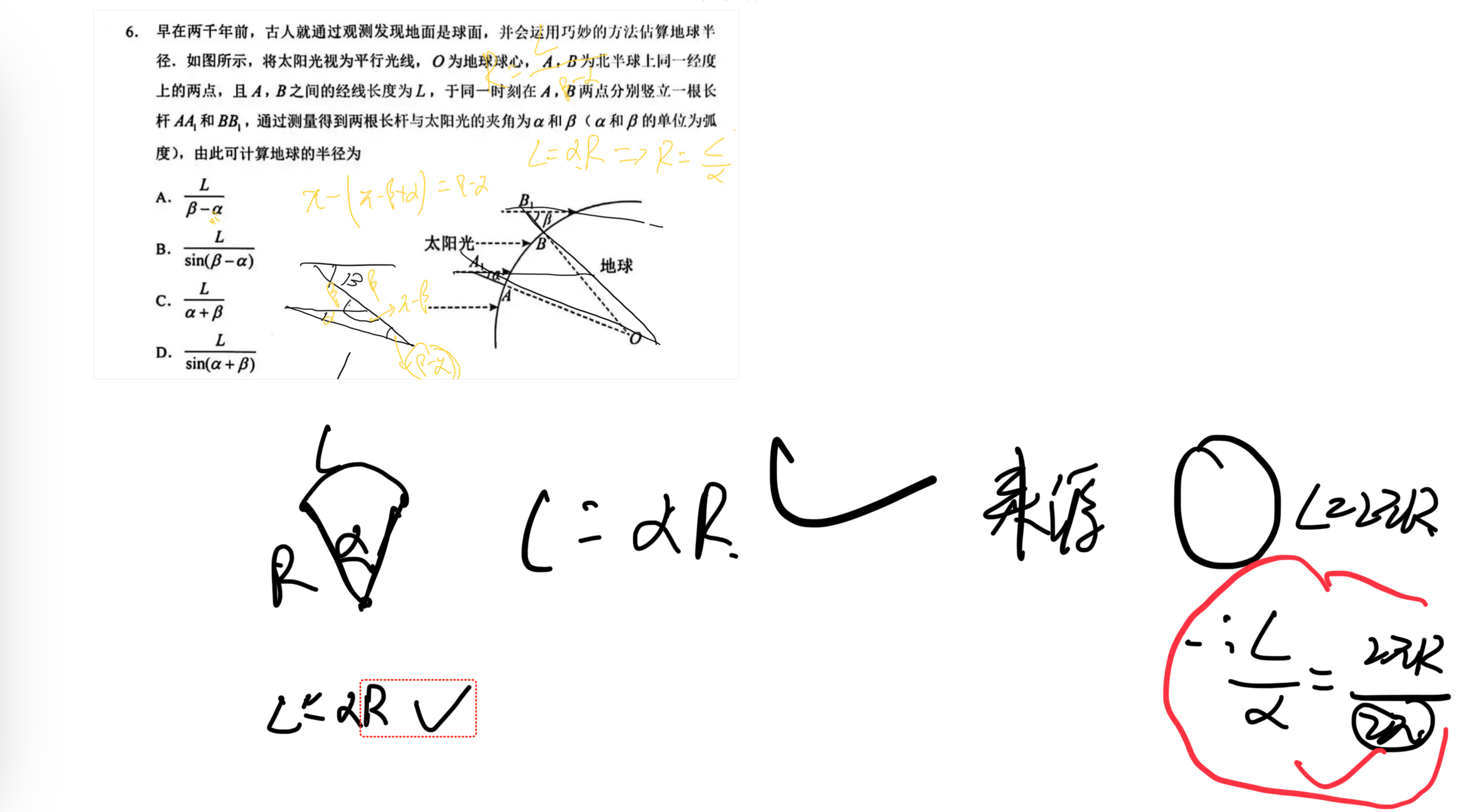
19压轴题

19.1圆锥曲线

椭圆 的某种给出办法

a半短轴 b半长轴 c焦点 椭圆上的一个点到两个焦点的距离和=2a (椭圆的定义)

本题运用相似三角形的知识