初等矩阵逆阵仍为初等矩阵且型不变

初等行变换与初等列变换合称为初等变换
解方程组禁止使用初等列变换!很简单的道理,把x1和x2的系数一换,方程组就变了

逆阵
逆阵的求法,可逆是前提 行列式不为0,旁边构造单位阵,将左边矩阵通过行变换变为单位阵,右侧矩阵即为原阵的逆矩阵 禁止列变换

回顾 左行 右列 ,三种类型初等矩阵 I交换两行 逆阵再次交换两行 ;II某行k倍 逆矩阵为 1/k倍; III i行k倍加到j行 逆矩阵为 -k倍
完整求逆阵流程,十分详细

秩 不要求方阵了
mxn的矩阵,其秩小于等于min{m,n}
定义 最重要的一句话: 两个条件,其一 存在r阶子式不为0 ,其二 对于任意的r+1阶子式,要么不存在要么为0
那么该矩阵的秩为r

特殊的,对于方阵,这个性质延展思考一下, 若该方阵可逆,那么行列式不为0,既然行列式不为0,则说明存在n阶子式不为0,且n+1阶子式不存在,那么这个矩阵的秩就是n,也称满秩
这是充要的,可以左右互推
当然,如果方阵不可逆,则说明降秩
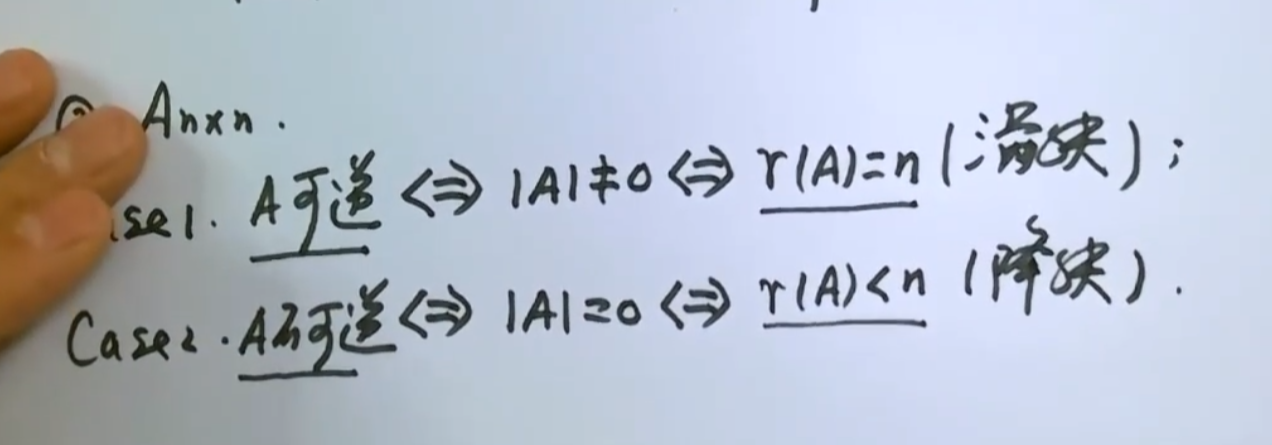
ra的求法? 肯定不能用定义去算,类似于求逆阵,一般不用A*定义去求 AA*=|A|E 最初的定义 可左乘矩阵变形得到A^{-1}=A* ·1/|A|
求秩还是用 初等行变换化行阶梯矩阵
后面第四节详细介绍秩的相关性质,运用到证明里



