
NLP – CQU软件学院

1 绪论 1.1基本概念 1.2NLP发展历史 1.3NLP研究内容 1.4NLP基本问题 1.5NLP面临的困难 1.6NLP基本研究方法 2 NLP前置数学基础 2.1 概率论基础 2.1.1概率 2.1.2 条件概率 2.1.3 贝叶斯公式 2.1.4 期望 2.1.5 二项分布 2.1.6 激活函数 2.1.7 最大似然估计 2.1.8 梯度下降 2.2 信息论基础 2.2.1 熵 entropy 2.2.2 联合熵 2.2.3 条件熵 2.2.4 熵的连锁反应 2.2.5 熵率 2.2.6 互信息 2.2.7 互信息与熵的关系 2.2.8 相对熵 2.2.9 交叉熵 2.2.10语言…
数据可视化
Anaconda

胡海波 主讲开卷首选教材 可视化导论 数据可视化 1 数据可视化简介 一、数据可视化:简介 1.1 数据可视化的定义P1 1.2 为什么要数据可视化P12P13P14P15P16P17P18 视觉是人类获取信息的重要通道P12P13 将数据映射成视觉形式P13 增强数据识别效率P15 高效传输有用信息P15 案例:Anscombe’s DataP16P17P18 案例:H. Rosling’s SpeakingP19 二、可视化:意义 & 作用 2.1 可视化的目标P22P23 传递信息P22P23P24 探索性P23P24 解释性P23P24 2.2 可视化的用途P25P26P27P…
用之前将cmd 初始化 conda init 创建环境? conda create --name py39 python=3.9 conda create --name py312 python=3.12 使用环境? conda activate py39 conda activate py312 查看已有环境 conda env list 2、powershell设置 conda init powershell Set-ExecutionPolicy -ExecutionPolicy RemoteSigned -Scope CurrentUser 3、取消一打开终端就默认进入conda的ba…

量化笔记
docker源搭建
CSharp基础
qnap nas 没有公网v4 如何实现外网访问内网
汇编指令
CQU DataMining复习 基于ppt

进阶平台 VeighNaPy VNPY 韦纳量化 Hikyuu Hikyuu - Quant Framework 下载数据 hikyuutdx 初始化 #在交互式环境下使用hikyuu,首先需引入hikyuu交互工具 from hikyuu.interactive.interactive import * Northstar 社区一般 盈富量化 java -jar "-Dloader.path=$(pwd)" -Denv=prod northstar-7.3.5.jar abu 很早就停止维护了 pythonstock 基于Docker 目前出现问题 2025-2-11 基础平台 (视频) Q…
涉及 VPS 编辑docker配置文件 配置nginx反向代理 配置域名解析
这篇文章没有摘要
这篇文章没有摘要
mozhongzhou: MessageBoxW ord:511 rva2iat: 0004D36C 解释 GitHub Copilot: MessageBoxW 是 Windows API 中的一个函数,用于显示一个包含消息和按钮的对话框。它的定义在 user32.dll 中。以下是对 MessageBoxW 的解释: 函数名: MessageBoxW 参数: hWnd: 父窗口的句柄。如果对话框没有父窗口,可以传递 NULL。 lpText: 显示在对话框中的消息文本。 lpCaption: 对话框的标题。 uType: 指定对话框的按钮和图标。 返回值: 用户点击的按钮。 ord:511…
1 数据 1. 数据概述 1.1 数据的概念:定义、分类(定性/定量、静态/动态、在线/离线等)P3P4 1.2 数据的分类:根据性质、时间、网络、位置、来源、范围、格式等进行分类P4 2. 数据内容 2.1 实时数据与历史数据:定义、特点、应用P5 2.2 时态数据与事务数据:定义、特点、区别P6P7 2.3 图形数据与图像数据:定义、特点、应用P8P9 2.4 主题数据与全部数据:定义、区别P10 2.5 空间数据:定义、分类(矢量/栅格)P11 2.6 序列数据和数据流:定义、特点P12 2.7 元数据和数据字典:定义、作用P13 3. 数据属性及数据集 3.1 数据属性:定义、分类(标…
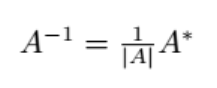
多元统计分析二轮复习 基于ppt
主成分分析 聚类分析 判别分析 H0 多元正态总体的统计推断 T方检验 1 矩阵代数 1.1定义 1.2矩阵运算 1.3行列式 1.4矩阵的逆 矩阵可逆便 行列式不为0 行列式不为0的矩阵叫非奇异矩阵 行列式为0的矩阵叫奇异矩阵 同时不可逆 用化最简行阶梯形也可以做 1.5矩阵的秩 1.6特征值,特征向量,矩阵的迹(这三个概念只有方阵才谈 矩阵的迹 1.7正定矩阵和非负定矩阵 顺序主子式 从矩阵左上角开始,按顺序取1阶、2阶...n阶的行列式 k阶顺序主子式是指:取矩阵左上角的k×k个元素构成的行列式 有趣的性质 主对角线的元素的绝对值 一定比该行 该列 所有其余元素绝对值之和还要大 第一章例…