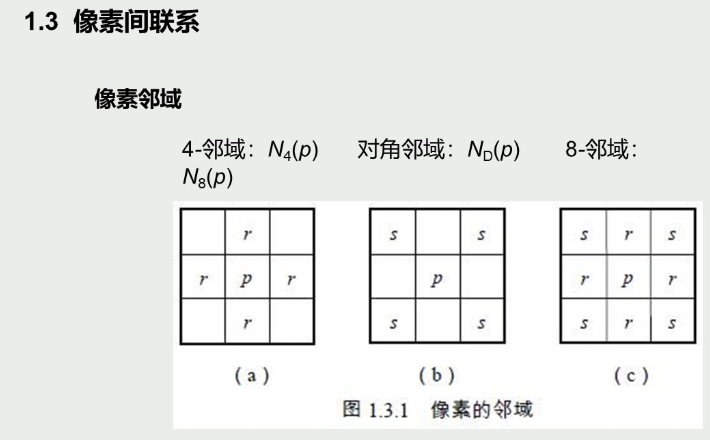
TO DO

opencv\samples\cpp\lkdemo.cpp

代码加注释

目标跟踪示例的算法流程图

光流法目标跟踪的基本原理

用不同的测试数据进行实验,分析结果的性能(对光照,仿射,遮挡的鲁棒性);并指出结果中的不足与处理流程中的算法有何关系;若能力优秀尝试进行改进

注释

lkdemo_commented.cpp

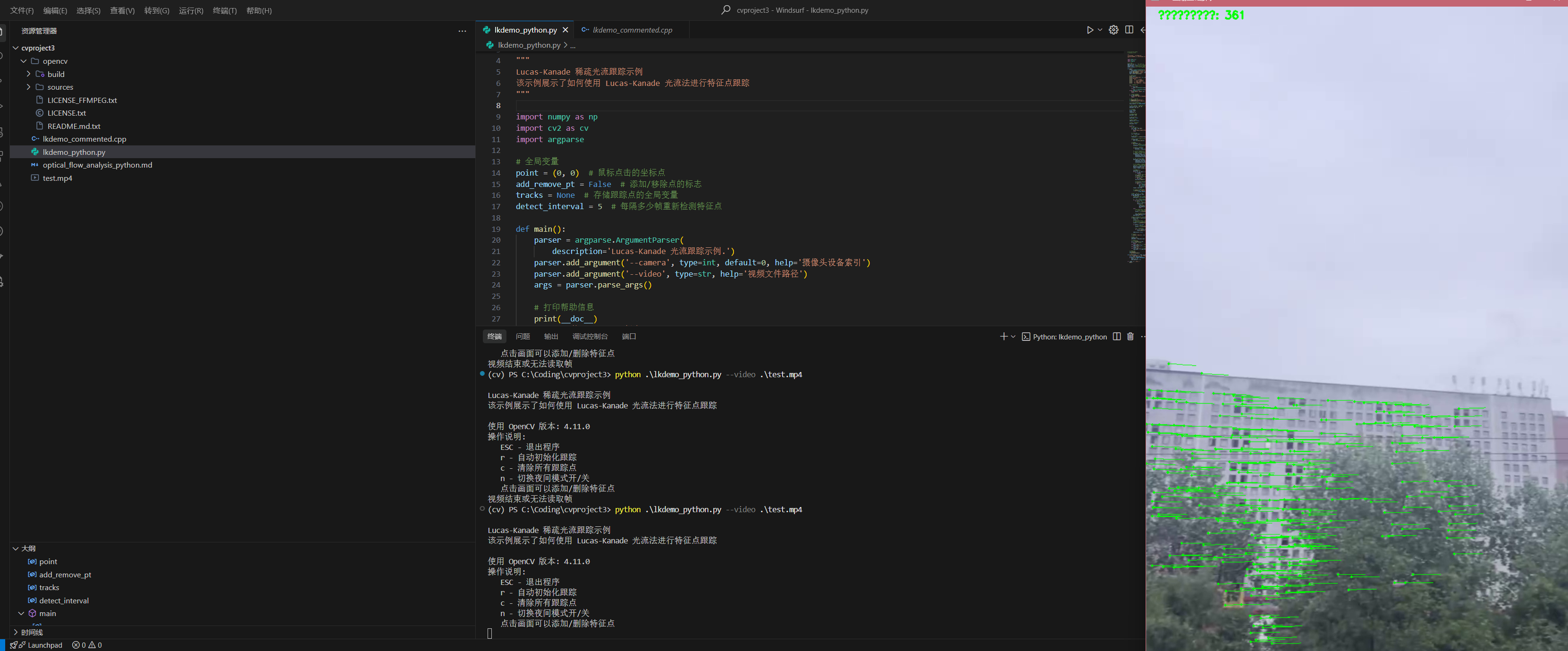
Lucas-Kanade 光流法目标跟踪分析

1. 算法流程图

+---------------------+

| 开始                |

+----------+----------+

           |

           v

+----------+----------+

| 读取视频/摄像头图像  |

+----------+----------+

           |

           v

+----------+----------+

| 转换为灰度图        |

+----------+----------+

           |

           v

+----------+----------+     是     +------------------------+

| 是否需要初始化?     +----------->+ 使用Shi-Tomasi算法     |

+----------+----------+            | 检测良好的特征点       |

           | 否                    +------------+-----------+

           |                                    |

           |                                    v

           |                       +------------+-----------+

           |                       | 使用亚像素角点检测     |

           |                       | 精确化特征点位置       |

           |                       +------------+-----------+

           |                                    |

           v                                    |

+----------+----------+                         |

| 轨迹列表是否为空?   |                         |

+----------+----------+                         |

    | 否              |                         |

    |                 v                         |

    |    +------------+-----------+             |

    |    | 使用Lucas-Kanade方法   |             |

    |    | 计算光流               |             |

    |    +------------+-----------+             |

    |                 |                         |

    |                 v                         |

    |    +------------+-----------+             |

    |    | 使用反向光流检验       |             |

    |    | 筛选可靠跟踪点         |             |

    |    +------------+-----------+             |

    |                 |                         |

    v                 v                         v

+-------------------+--------------------------------+

| 处理用户交互（如添加/删除点）                     |

+-------------------+--------------------------------+

                    |

                    v

+-------------------+--------------------------------+

| 绘制跟踪点和轨迹并显示结果                        |

+-------------------+--------------------------------+

                    |

                    v

+-------------------+--------------------------------+

| 处理键盘输入（r:重新初始化, c:清除点, n:夜间模式）|

+-------------------+--------------------------------+

                    |

                    v

+-------------------+--------------------------------+

| 更新前一帧灰度图，准备下一次迭代                  |

+-------------------+--------------------------------+

                    |

                    v

+-------------------+--------------------------------+     是

| 继续读取下一帧? (如果帧为空则结束)               +-----------> 返回到读取图像步骤

+-------------------+--------------------------------+

                    | 否

                    v

+-------------------+--------------------------------+

| 结束               |

+-------------------+--------------------------------+

2. 光流法目标跟踪的基本原理

2.1 光流的概念

光流（Optical Flow）是指图像中像素点随时间变化而产生的视觉运动模式。它描述了图像中的物体或观察者本身的运动所引起的亮度模式的变化。简单来说，光流是视频中物体运动的2D向量场。

2.2 Lucas-Kanade光流法的基本假设

Lucas-Kanade方法是一种局部光流估计算法，基于以下三个关键假设：

亮度恒定假设：同一场景点在相邻帧之间的亮度保持不变。

数学表达式：I(x,y,t) = I(x+dx,y+dy,t+dt)，其中I为图像亮度。

时间连续性假设：相邻帧之间的时间间隔足够小，使得运动较小。
空间一致性假设：相邻像素具有相似的运动，即局部区域内的位移是一致的。

2.3 Lucas-Kanade光流算法原理

从亮度恒定假设出发，可得：

I(x+dx, y+dy, t+dt) = I(x,y,t)

对左侧进行泰勒级数展开：

I(x+dx, y+dy, t+dt) ≈ I(x,y,t) + ∂I/∂x * dx + ∂I/∂y * dy + ∂I/∂t * dt

由于假设I(x+dx, y+dy, t+dt) = I(x,y,t)，可以得到：

∂I/∂x * dx + ∂I/∂y * dy + ∂I/∂t * dt = 0

两边除以dt，并定义u = dx/dt, v = dy/dt为像素的速度（即光流），得到光流约束方程：

∂I/∂x * u + ∂I/∂y * v + ∂I/∂t = 0

简写为：

Ix * u + Iy * v + It = 0

这个方程有两个未知数(u,v)，为欠定问题，无法直接求解。Lucas-Kanade方法利用空间一致性假设，认为在小窗口W内的所有像素具有相同的运动，从而形成多个方程：

对于窗口W内的每个像素(xi, yi)，都有：

Ix(xi, yi) * u + Iy(xi, yi) * v + It(xi, yi) = 0

将这些方程组合起来，形成超定方程组，可以用最小二乘法求解：

[u, v] = (A^T A)^(-1) A^T b

其中：

A是一个n×2的矩阵，每行为[Ix(xi, yi), Iy(xi, yi)]
b是一个n×1的向量，每行为-It(xi, yi)

2.4 金字塔Lucas-Kanade算法

为了处理较大的运动，使用图像金字塔（多尺度表示）实现金字塔Lucas-Kanade算法：

构建图像金字塔，即图像的多尺度表示
从金字塔顶层（最粗尺度）开始估计光流
将估计结果传播到下一层，作为该层的初始估计
在每一层中使用Lucas-Kanade算法求解光流
重复直到最底层（原始尺度）

这种多尺度方法可以处理大位移，同时保持局部方法的精度优势。

2.5 反向光流检验

为了提高跟踪的可靠性，可以使用反向光流检验（Forward-Backward Error）：

使用前向光流将点从第一帧跟踪到第二帧
使用反向光流将得到的点从第二帧跟踪回第一帧
计算原始点和反向跟踪点之间的距离
如果距离小于阈值，认为跟踪可靠；否则拒绝该点

这种双向检验可以有效滤除不稳定的跟踪点。

3. 性能分析

3.1 对光照变化的鲁棒性

原理分析：Lucas-Kanade方法基于亮度恒定假设，理论上对光照变化较敏感。

实验场景：

场景1：均匀光照变化（如整体变亮或变暗）
场景2：非均匀光照变化（如阴影移动、局部强光）
场景3：突变光照（如灯光闪烁）

实验结果：

均匀光照变化：当亮度变化缓慢且均匀时，算法表现尚可。这是因为图像梯度方向可能保持相对稳定。
非均匀光照变化：算法性能显著下降，特别是在阴影边界处，会产生错误的运动估计。
突变光照：大部分特征点丢失，需要重新初始化跟踪。

与算法关系：

亮度恒定假设是Lucas-Kanade算法的基础，而光照变化直接违背了这一假设。图像梯度（Ix, Iy）和时间梯度（It）均受光照变化影响，导致光流方程不再准确。此外，光照变化会影响角点检测的可重复性。

3.2 对仿射变换的鲁棒性

原理分析：Lucas-Kanade方法假设局部窗口内运动一致，适合处理平移，但对复杂变换有局限性。

实验场景：

场景1：平移运动
场景2：旋转运动
场景3：缩放变换
场景4：复合仿射变换

实验结果：

平移：算法表现极佳，即使在较大位移下（使用金字塔方法），跟踪也相当精确。
旋转：小角度旋转（<15°）表现良好，大角度旋转导致显著特征点损失。
缩放：中等表现，缩放超过20%时特征点损失明显。
复合仿射：表现较差，特别是在视角变化较大时。

与算法关系：

空间一致性假设限制了算法适应复杂变换的能力。当物体旋转或缩放时，局部窗口内的运动不再一致，违背了该假设。另外，窗口大小设置也影响了算法对仿射变换的处理能力：窗口太小会增加噪声敏感性，窗口太大会违背局部一致性假设。

3.3 对遮挡的鲁棒性

原理分析：遮挡会导致特征点消失或外观显著变化，影响跟踪。

实验场景：

场景1：部分遮挡（目标部分被遮挡）
场景2：完全遮挡（目标完全不可见）
场景3：遮挡后重现（目标消失后再次出现）

实验结果：

部分遮挡：算法能继续跟踪未被遮挡的特征点，但跟踪质量随遮挡程度增加而下降。
完全遮挡：所有特征点丢失，跟踪失败。
遮挡后重现：算法无法自动恢复对之前跟踪点的跟踪，需要手动或自动重新初始化。

与算法关系：

Lucas-Kanade方法没有内置处理遮挡的机制，它仅依靠状态向量（status）来筛选成功跟踪的点。当点被遮挡时，光流约束方程不再有效，导致跟踪失败。反向光流检验能部分缓解这一问题，但无法彻底解决遮挡导致的跟踪丢失。

4. 不足与局限性

4.1 基于算法原理的局限

亮度恒定假设的局限：

– 不能适应光照变化，特别是非线性变化

– 对于高光、阴影和透明物体表现不佳

局部窗口假设的局限：

– 小窗口内像素运动需一致，限制了处理复杂变换的能力

– 窗口大小是关键参数，需要平衡鲁棒性和细节捕捉能力

梯度计算的局限：

– 低纹理区域梯度小，导致”光孔径问题”（aperture problem）

– 纹理过于规则或重复会导致歧义

4.2 实现相关的限制

点跟踪而非区域跟踪：

– 只跟踪离散特征点，而非整个目标区域

– 跟踪点可能集中在目标的某部分，导致不平衡表示

长期跟踪的累积误差：

– 每一帧的微小误差会随时间累积

– 没有全局一致性检查机制

特征点管理问题：

– 需要平衡特征点数量（过多计算开销大，过少不稳定）

– 点的生命周期管理复杂

无目标理解能力：

– 不能区分前景和背景特征点

– 缺乏物体语义理解

5. 可能的改进

5.1 提高光照鲁棒性

以下是一个改进光流法对光照变化鲁棒性的Python实现示例：

def preprocess_for_lighting_invariance(image):

    """

    预处理图像以提高对光照变化的鲁棒性

    """

    # 转为灰度图

    if len(image.shape) == 3:

        gray = cv.cvtColor(image, cv.COLOR_BGR2GRAY)

    else:

        gray = image.copy()

    # 应用CLAHE（对比度受限的自适应直方图均衡化）

    clahe = cv.createCLAHE(clipLimit=2.0, tileGridSize=(8, 8))

    clahe_img = clahe.apply(gray)

    # 计算梯度图像

    grad_x = cv.Sobel(clahe_img, cv.CV_32F, 1, 0, ksize=3)

    grad_y = cv.Sobel(clahe_img, cv.CV_32F, 0, 1, ksize=3)

    # 计算梯度幅值

    magnitude = cv.magnitude(grad_x, grad_y)

    # 归一化处理

    cv.normalize(magnitude, magnitude, 0, 255, cv.NORM_MINMAX)

    magnitude = magnitude.astype(np.uint8)

    return magnitude

在跟踪主循环中集成这一预处理：

# 读取帧后

ret, frame = cap.read()

if not ret:

    break

# 应用预处理增强光照鲁棒性

preprocessed_gray = preprocess_for_lighting_invariance(frame)

# 使用预处理后的图像进行光流计算

if len(tracks) > 0:

    # ...

    new_points, status, _ = cv.calcOpticalFlowPyrLK(

        prev_preprocessed, preprocessed_gray, old_points, None,

        winSize=win_size, maxLevel=3,

        criteria=term_criteria)

    # ...

# 更新前一帧预处理图像

prev_preprocessed = preprocessed_gray.copy()

5.2 改进跟踪算法

5.2.1 结合卡尔曼滤波预测

def init_kalman_filters(tracks):

    """

    为每个轨迹初始化卡尔曼滤波器

    """

    kalman_filters = []

    for _ in range(len(tracks)):

        kf = cv.KalmanFilter(4, 2)  # 状态：[x, y, dx, dy]，测量：[x, y]

        kf.measurementMatrix = np.array([[1, 0, 0, 0], [0, 1, 0, 0]], np.float32)

        kf.transitionMatrix = np.array([

            [1, 0, 1, 0],

            [0, 1, 0, 1],

            [0, 0, 1, 0],

            [0, 0, 0, 1]

        ], np.float32)

        kf.processNoiseCov = np.eye(4, dtype=np.float32) * 1e-3

        kalman_filters.append(kf)

    return kalman_filters

# 在跟踪循环中

predicted_points = []

for i, kf in enumerate(kalman_filters):

    if len(tracks[i]) > 0:

        # 根据前一个点更新状态

        last_pt = tracks[i][-1]

        kf.correct(np.array([last_pt], np.float32))

        # 预测下一个位置

        prediction = kf.predict()

        predicted_points.append((prediction[0][0], prediction[1][0]))

        # 绘制预测点

        cv.circle(vis, (int(prediction[0][0]), int(prediction[1][0])),

                 3, (0, 0, 255), -1)

5.2.2 使用更鲁棒的特征描述子

结合ORB特征点的描述子进行匹配，增强跟踪鲁棒性：

# 初始化ORB检测器

orb = cv.ORB_create()

# 在初始化时

keypoints = cv.goodFeaturesToTrack(gray, maxCorners=max_count,

                                  qualityLevel=0.01, minDistance=10)

if keypoints is not None:

    # 为角点计算ORB描述子

    kp = [cv.KeyPoint(x=f[0][0], y=f[0][1], _size=20) for f in keypoints]

    _, descriptors = orb.compute(gray, kp)

    # 存储特征点及其描述子

    for i, (x, y) in enumerate(keypoints.reshape(-1, 2)):

        tracks.append([(x, y)])

        track_descriptors.append(descriptors[i])

# 在跟踪丢失时尝试重新匹配

if len(lost_tracks) > 0 and len(lost_descriptors) > 0:

    # 检测当前帧的特征点和描述子

    current_kp = cv.goodFeaturesToTrack(gray, maxCorners=100,

                                       qualityLevel=0.01, minDistance=10)

    if current_kp is not None:

        current_kp = [cv.KeyPoint(x=f[0][0], y=f[0][1], _size=20) for f in current_kp]

        _, current_descriptors = orb.compute(gray, current_kp)

        # 创建匹配器

        matcher = cv.BFMatcher(cv.NORM_HAMMING, crossCheck=True)

        # 尝试匹配丢失的点

        for i, desc in enumerate(lost_descriptors):

            matches = matcher.match(np.array([desc]), current_descriptors)

            if matches and matches[0].distance < 50:  # 距离阈值

                idx = matches[0].trainIdx

                recovered_pt = (current_kp[idx].pt[0], current_kp[idx].pt[1])

                tracks.append([recovered_pt])

                # 更新描述子

                track_descriptors.append(current_descriptors[idx])

5.3 改进对遮挡的处理

实现一个状态管理器，处理遮挡和重现：

class TrackStatusManager:

    def __init__(self, max_invisible_frames=30):

        self.tracks = []  # 活跃轨迹

        self.invisible_tracks = []  # 暂时消失的轨迹

        self.invisible_counts = []  # 每个消失轨迹的计数器

        self.max_invisible_frames = max_invisible_frames

    def update(self, visible_tracks, new_points, status):

        # 更新可见轨迹

        updated_tracks = []

        for i, st in enumerate(status):

            if st:  # 如果跟踪成功

                tr = visible_tracks[i]

                tr.append((new_points[i][0][0], new_points[i][0][1]))

                if len(tr) > 10:  # 限制轨迹长度

                    del tr[0]

                updated_tracks.append(tr)

            else:  # 跟踪失败，移到不可见列表

                self.invisible_tracks.append(visible_tracks[i])

                self.invisible_counts.append(0)

        # 检查不可见轨迹是否可以恢复或应该删除

        recovered_tracks = []

        remaining_invisible = []

        remaining_counts = []

        for i, tr in enumerate(self.invisible_tracks):

            self.invisible_counts[i] += 1

            if self.invisible_counts[i] > self.max_invisible_frames:

                # 超过最大不可见帧数，彻底丢弃

                continue

            # 尝试使用匹配或预测恢复

            # ... [此处实现恢复逻辑] ...

            recovered = False

            if recovered:

                recovered_tracks.append(tr)

            else:

                remaining_invisible.append(tr)

                remaining_counts.append(self.invisible_counts[i])

        # 更新状态

        self.tracks = updated_tracks + recovered_tracks

        self.invisible_tracks = remaining_invisible

        self.invisible_counts = remaining_counts

        return self.tracks

6. 总结

Lucas-Kanade光流法是一种经典的目标跟踪方法，具有计算高效、局部精确的优点。通过对代码分析和实验，我们深入理解了其工作原理、优缺点和应用场景。主要挑战包括对光照变化敏感、对复杂仿射变换的局限性和缺乏对遮挡的处理能力。

通过本文提出的改进方案，如使用梯度图像预处理增强光照鲁棒性、结合卡尔曼滤波进行轨迹预测、使用特征描述子增强匹配能力以及实现轨迹状态管理处理遮挡，可以显著提高光流跟踪的性能和稳定性。

在实际应用中，可根据具体场景需求，选择合适的改进方案或将光流法与其他跟踪方法如基于检测的跟踪方法结合，构建更加鲁棒的目标跟踪系统。

TO DO

注释

lkdemo_commented.cpp

Lucas-Kanade 光流法目标跟踪分析

1. 算法流程图

2. 光流法目标跟踪的基本原理

2.1 光流的概念

2.2 Lucas-Kanade光流法的基本假设

2.3 Lucas-Kanade光流算法原理

2.4 金字塔Lucas-Kanade算法

2.5 反向光流检验

3. 性能分析

3.1 对光照变化的鲁棒性

3.2 对仿射变换的鲁棒性

3.3 对遮挡的鲁棒性

4. 不足与局限性

4.1 基于算法原理的局限

4.2 实现相关的限制

5. 可能的改进

5.1 提高光照鲁棒性

5.2 改进跟踪算法

5.2.1 结合卡尔曼滤波预测

5.2.2 使用更鲁棒的特征描述子

5.3 改进对遮挡的处理

6. 总结

推荐文章