学习框架
1. 基础知识准备
在学习计算机视觉之前,需要打好数学和编程的理论基础,这些是后续学习的核心支撑。
- 数学基础:
- 线性代数:掌握矩阵、向量、特征值和特征向量等概念,这些在图像变换和特征提取中非常重要。
- 微积分:理解梯度、偏导数和优化方法,用于模型训练和图像处理。
- 概率论与统计学:熟悉条件概率、贝叶斯定理和随机变量的基本知识,帮助理解机器学习模型。
- 编程技能:
- 建议熟练掌握Python,因为它在计算机视觉领域有广泛的库支持(如OpenCV、TensorFlow、PyTorch)。C++也是一个可选语言,尤其在性能优化时有用。
2. 图像处理基础
理解图像的表示和基本处理技术是CV的入门步骤。
- 图像表示:
- 学习图像的数字表示方式,例如像素、颜色空间(RGB、HSV、灰度)和常见图像格式(JPEG、PNG)。
- 图像处理技术:
- 滤波:如高斯滤波、中值滤波,用于图像平滑或去噪。
- 边缘检测:如Sobel算子、Canny算法,用于提取图像边缘特征。
- 图像变换:如傅里叶变换(分析频率信息)、霍夫变换(检测直线或圆形)。
3. 特征提取与描述
特征提取是传统计算机视觉的核心,用于从图像中提取有用的信息。
- 局部特征:
- 学习SIFT、SURF、ORB等算法,用于检测和描述图像中的关键点。
- 全局特征:
- 了解颜色直方图、纹理特征等全局描述方法。
- 特征匹配:
- 掌握最近邻匹配和RANSAC算法,用于在不同图像间建立对应关系。
4. 机器学习与深度学习基础
现代计算机视觉离不开机器学习和深度学习的支持。
- 机器学习:
- 理解监督学习、无监督学习和强化学习的基本概念。
- 深度学习:
- 学习神经网络的基本原理,尤其是卷积神经网络(CNN),它是CV任务的主流工具。
- 框架掌握:
- 熟练使用TensorFlow或PyTorch等深度学习框架,加速模型开发和实验。
5. 计算机视觉中的深度学习
深度学习在CV中的应用推动了图像分类、目标检测和分割等任务的突破。
- 图像分类:
- 使用CNN进行分类,学习经典网络如LeNet、AlexNet、VGG、ResNet。
- 目标检测:
- 掌握R-CNN、Faster R-CNN、YOLO、SSD等算法,用于识别图像中的物体及其位置。
- 图像分割:
- 学习语义分割(FCN、U-Net)和实例分割(Mask R-CNN)技术。
- 其他任务:
- 探索图像生成(GANs)、风格迁移和超分辨率等前沿应用。
6. 高级主题与应用
深入学习CV的高级领域,扩展到三维视觉和视频分析。
- 三维视觉:
- 研究立体视觉、结构光和SLAM(同时定位与地图构建)。
- 视频分析:
- 学习运动估计、光流计算和行为识别。
- 应用场景:
- 了解CV在自动驾驶、机器人视觉等领域的结合。
7. 实践与项目
理论结合实践是学习CV的关键。
- 数据集:
- 熟悉 ImageNet、COCO、Pascal VOC 等常用数据集。
- 项目实践:
- 实现图像分类器、物体检测器或图像分割工具,巩固所学知识。
- 论文阅读:
- 阅读CV领域的最新研究论文,跟踪技术前沿。
1 导论
视觉和视知觉?
形状的感知?
边缘检测?
轮廓对应亮度的二阶导数?
全是废话
1.2 图像基础
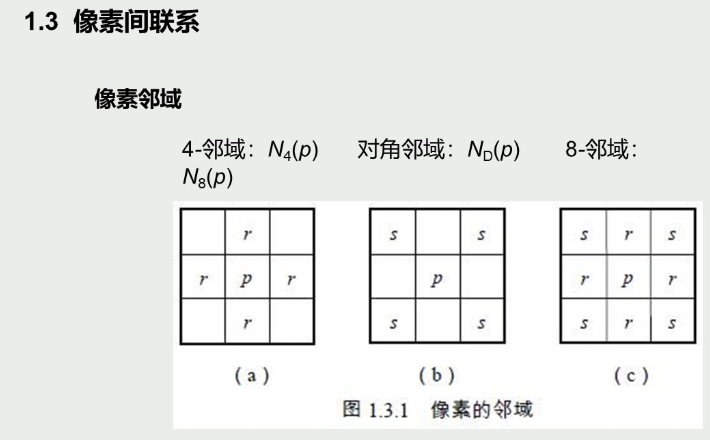

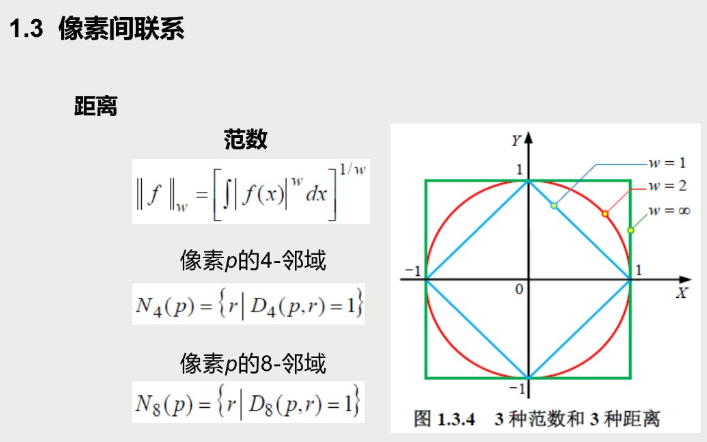
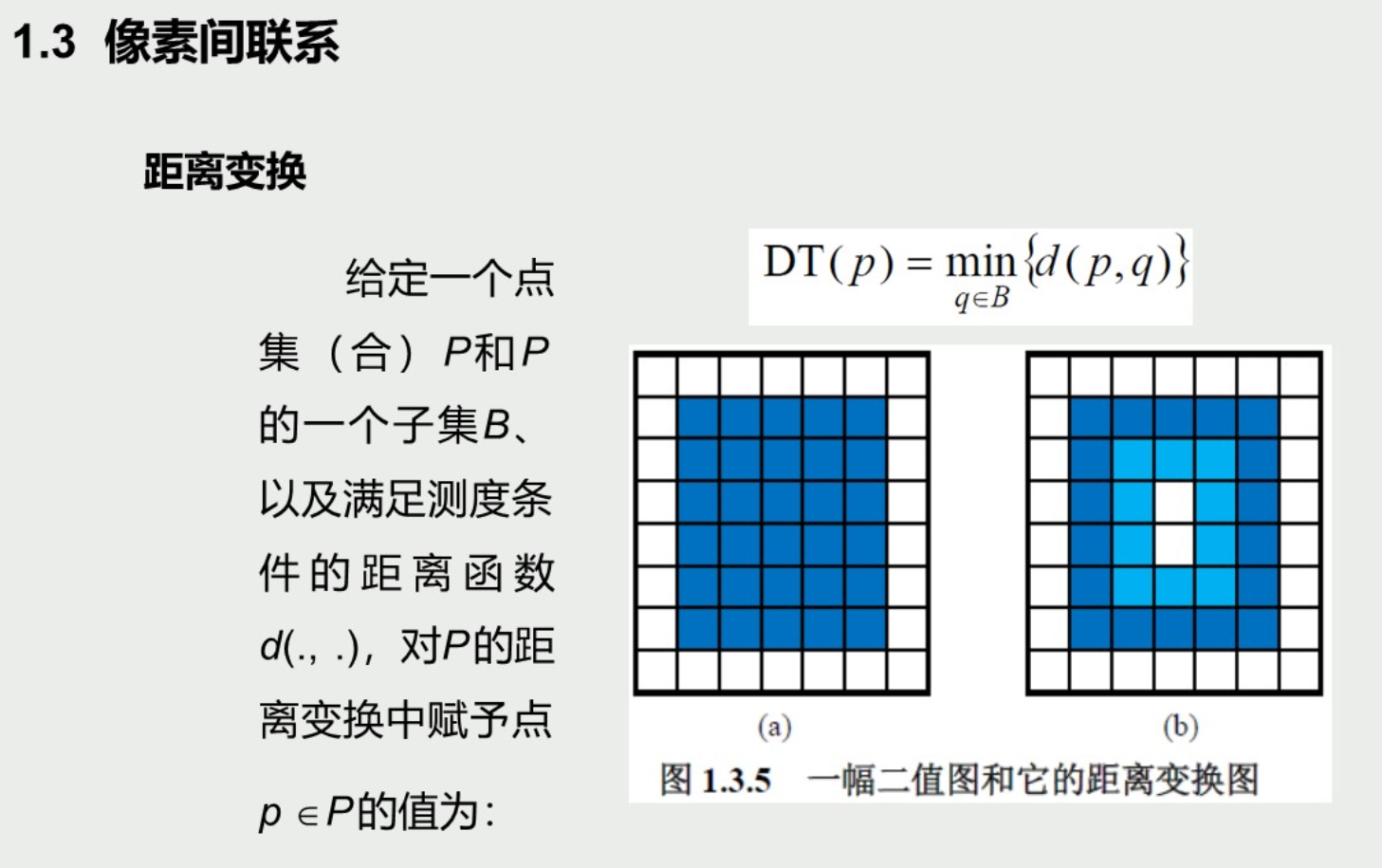
例题 比如算D8的和 可以直接在这个像素上写数字 第一列全是1; 第二列左右为1 中间为2 ;以此类推
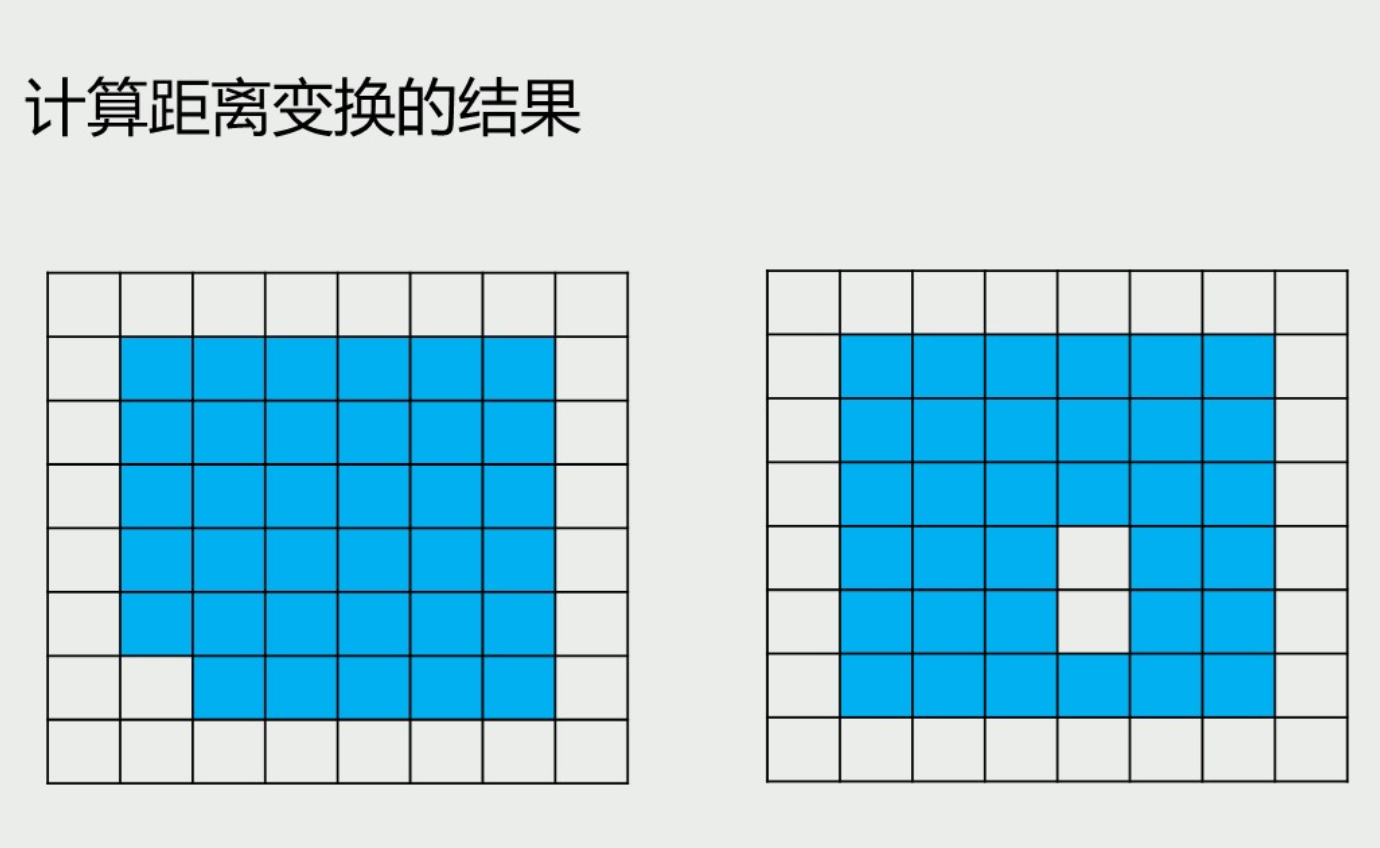
图像预处理?
图像坐标变换
灰度映射
直方图修正(important)
??
直方图变换
??
灰度直方图
直方图均衡化
直方图规定化
空域滤波
图像变换技术
几何变换
基本变换

灰度插值
非几何变换
灰度映射
直方图变换
模板运算
图像的频域变换
傅里叶变换?
频域常用于去除噪点 (高频?)
基本坐标变换??????????????
没学过计算机图形学,图像处理,数字信号处理,能否学计算机视觉? 会有哪些难点?
向前映射计算法
从原图像坐标计算出目标图像坐标
向后映射计算法
从结果图像的坐标计算原图像的坐标 倒推
最近邻插值法?
直方图均衡化
L是8 应该是叫分的几个层次数量 在这里分为0,1,2,3,4,5,6,7 一共八个层次 所以L=8
注意下面序号4 +0.5 说白了为了四舍五入
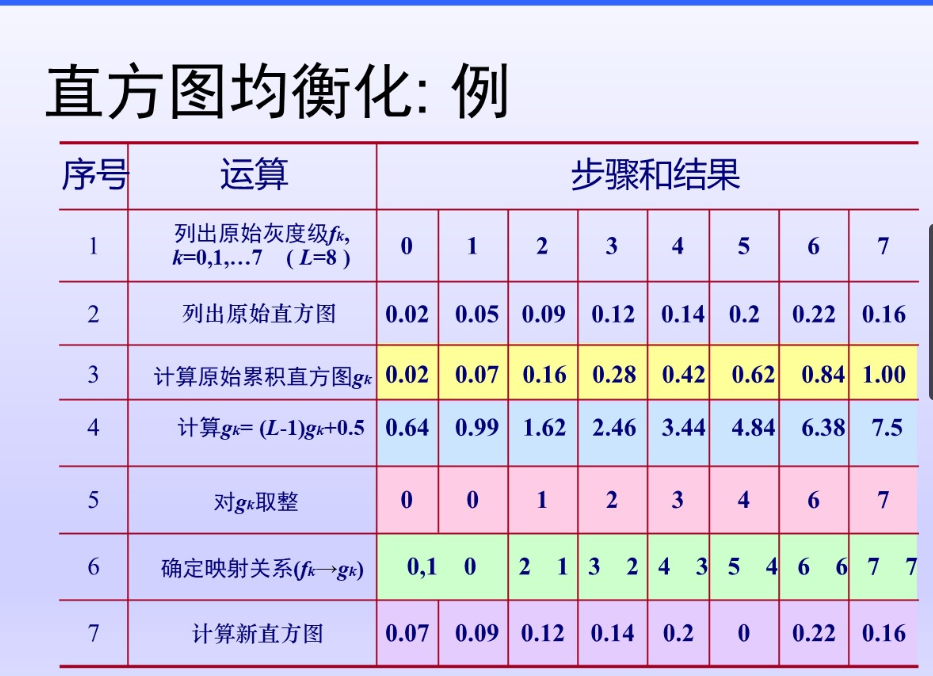
直方图规定化


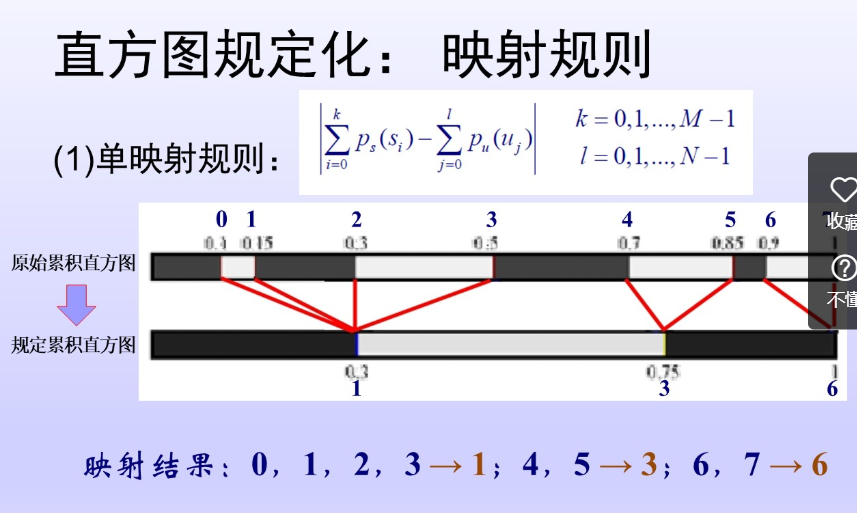
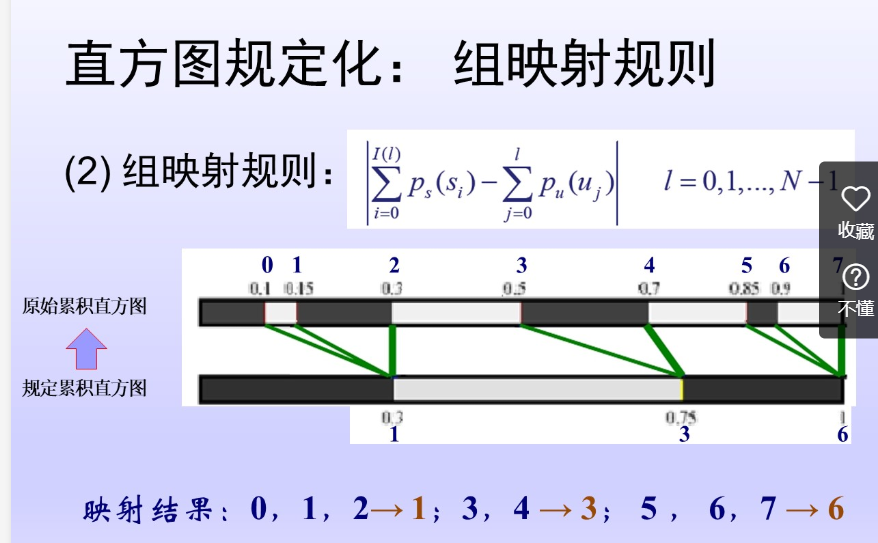
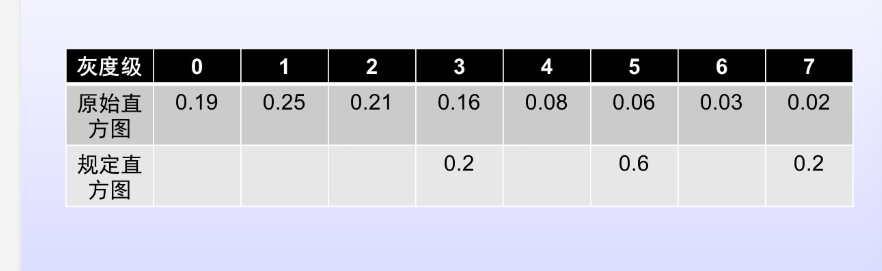
先求累计直方图
原始直方图的累计直方图:0.19 0.44 0.65 0.81 0.89 0.95 0.98 1
规定直方图的累计直方图:0.2 0.8 1
单映射 0,1 ->3 ; 2,3,4->5 ; 5,6,7->7
组映射 0->3 ; 1,2->5 ; 3,4,5,6,7->7

图像特征 Image Features
图像特征检测与描述
在计算机视觉领域,flat、edge和corner是描述图像中像素区域特征的三个基本概念,主要是从局部梯度变化的角度来区分的,具体区别如下:
1️⃣ Flat(平坦区域)
定义:
图像中的像素值几乎没有变化,灰度值非常接近或相同,整体是平滑的。
特点:
- 梯度变化非常小或接近0。
- 没有明显的纹理或边缘。
- 像是一片纯色区域,信息量低。
示例:
- 纯色背景。
- 天空、墙面等大块单色区域。
2️⃣ Edge(边缘)
定义:
图像中像素值沿某个方向发生剧烈变化,通常是物体边界或表面纹理的边界。
特点:
- 梯度在某个方向上非常大,说明沿该方向像素变化剧烈。
- 垂直于边缘的方向梯度大,平行方向梯度小。
- 信息量比 flat 高,但方向性强(只在一个方向上变化)。
示例:
- 物体边缘。
- 黑白交界线。
3️⃣ Corner(角点)
定义:
图像中像素值沿多个方向都发生剧烈变化的点,通常是两个或多个边缘交汇的地方。
特点:
- 梯度在多个方向都很大。
- 局部区域内信息丰富。
- 特殊点,通常对跟踪和匹配非常有用(如Harris角点检测)。
示例:
- 矩形物体的顶点。
- 窗户的四角。
总结对比
| 特征 | 梯度大小 | 变化方向 | 信息量 | 典型位置 |
|---|---|---|---|---|
| Flat | 近似为0 | 无 | 低 | 纯色区域 |
| Edge | 单方向大 | 单方向 | 中 | 物体边缘 |
| Corner | 多方向大 | 多方向 | 高 | 物体角点 |
简单理解
- Flat:光滑无变化
- Edge:单方向剧烈变化(边)
- Corner:多方向剧烈变化(角)
Hessian矩阵和行列式的区别
1️⃣ Hessian Matrix(Hessian矩阵)
定义
Hessian矩阵是一个二阶偏导数矩阵,描述函数(或图像灰度)的局部二阶变化率。在图像处理中,假设III是图像灰度值函数,那么二维Hessian矩阵形式是:H=[IxxIxyIxyIyy]H = \begin{bmatrix} I_{xx} & I_{xy} \\ I_{xy} & I_{yy} \end{bmatrix}H=[IxxIxyIxyIyy]
- IxxI_{xx}Ixx:x方向二阶导数
- IyyI_{yy}Iyy:y方向二阶导数
- IxyI_{xy}Ixy:x和y方向的混合二阶导数(交叉导数)
作用
- 描述图像的局部曲率。
- 在特征检测中,反映某点周围的几何特性。
- 是描述局部特征强弱的重要工具。
2️⃣ Hessian Determinant(Hessian行列式)
定义
Hessian determinant 是Hessian矩阵的行列式,也就是:Det(H)=Ixx⋅Iyy−(Ixy)2\text{Det}(H) = I_{xx} \cdot I_{yy} – (I_{xy})^2Det(H)=Ixx⋅Iyy−(Ixy)2
作用
- 用一个数值来综合描述Hessian矩阵的特征。
- 衡量局部特征点的强度。
- 在特征点检测中,Hessian determinant 越大,特征越明显。
3️⃣ 关键区别总结
| 对比项 | Hessian Matrix | Hessian Determinant |
|---|---|---|
| 定义 | 二阶偏导数组成的矩阵 | Hessian矩阵的行列式(一个数) |
| 形式 | 矩阵 | 数值 |
| 信息量 | 包含全部二阶信息 | 仅总结整体变化强度 |
| 主要作用 | 描述局部二阶变化的方向和大小 | 用一个值描述特征点强弱 |
| 维度 | 2×2(图像常见)或n×n | 单个标量 |
| 应用 | 图像特征描述、特征方向估计 | 特征点检测、特征强度排序 |
Hessian矩阵(Hessian Matrix)和Harris角点检测(Harris Corner Detection)
| 对比维度 | Hessian矩阵 | Harris方法 |
|---|---|---|
| 核心思路 | 利用二阶导数检测特征点(曲率变化) | 利用一阶导数检测特征点(梯度变化) |
| 数学工具 | Hessian矩阵 | 结构张量(也叫二阶矩阵 M,是梯度的外积积分) |
| 关注重点 | 直接通过Hessian行列式判断特征点强度 | 通过窗口内的梯度变化响应值 R判断特征点强度 |
| 适用场景 | 边缘/角点检测都可(SURF等算法用它) | 主要用于角点检测(Harris Corner Detector) |
| 计算复杂度 | 相对高(要算二阶导) | 相对低(只算一阶导) |
| 对噪声敏感度 | 对噪声相对敏感 | 对噪声较鲁棒(引入高斯平滑) |
| 特征点分布 | 可能检测到更多边缘点 | 更关注真正的角点,过滤边缘点 |
| 代表算法 | SURF(加速鲁棒特征) | Harris角点检测 |
图像特征检测算法
Rog 和Dog detector是什么
ChatGPT 说:
RoG (Region of Gradient) detector 和 DoG (Difference of Gaussian) detector 都是常见的用于图像特征检测的算法,尤其是在计算机视觉领域,它们常常被用于角点、边缘检测和尺度不变特征提取。下面我将分别解释它们的原理和应用。
1. RoG Detector (Region of Gradient)
Region of Gradient (RoG) 是一种基于图像梯度(灰度变化)的特征检测方法,它通过寻找图像中的梯度区域(即图像中灰度变化比较大的区域)来识别特征。这种方法的核心思想是利用梯度信息找到图像中重要的区域,这些区域通常对应于图像中的边缘或角点。
- 工作原理: RoG 检测器通过计算图像中每个点的梯度来判断该点是否是一个“关键”区域。图像中的梯度表示了图像灰度变化的强度,通常在图像的边缘和纹理区域,梯度值会较大,因此可以用来检测图像中的边缘特征。
- 应用: RoG 可以用来检测图像中的边缘、纹理,或者作为其他算法(如 SIFT、SURF 等)中检测关键点的辅助工具。
2. DoG Detector (Difference of Gaussian)
Difference of Gaussian (DoG) 是一种常用于特征检测(特别是角点检测)的算法,它是一种通过对图像进行高斯滤波处理后,计算两种不同标准差的高斯模糊图像之间的差值来检测图像中显著特征的方式。
- 工作原理: DoG 检测的核心思想是,通过对图像应用两种不同标准差的高斯滤波器 $σ1\sigma_1σ1 和 σ2\sigma_2σ2$,计算得到两个高斯模糊图像的差值:$DoG(x,y,σ)=G(x,y,σ1)−G(x,y,σ2)DoG(x, y, \sigma) = G(x, y, \sigma_1) – G(x, y, \sigma_2)DoG(x,y,σ)=G(x,y,σ1)−G(x,y,σ2)其中,G(x,y,σ)G(x, y, \sigma)G(x,y,σ) $是高斯滤波器,$σ1\sigma_1σ1 和 σ2\sigma_2σ2$ 是不同的标准差。差值图像中,图像的显著区域(如边缘、角点)会被突出显示。这是因为在图像的不同尺度上,显著特征会在高斯滤波后的图像中产生较大的差异。
- 应用:
- 边缘和角点检测:DoG 广泛应用于图像的多尺度特征检测中,特别是在如 SIFT(尺度不变特征变换)等算法中,DoG 用来检测不同尺度下的特征点。
- 尺度空间理论:DoG 是尺度空间中的一个重要方法,通过不同的尺度空间来检测图像的多尺度特征,从而实现尺度不变的特征点检测。
RoG 和 DoG 主要区别:
- 原理不同:RoG 主要依赖梯度信息,检测图像中灰度变化剧烈的区域,而 DoG 是基于高斯滤波计算两种不同尺度图像的差值。
- 应用场景:RoG 适用于寻找图像的局部变化区域(如边缘、纹理),而 DoG 适用于在不同尺度下检测图像的显著特征(如角点、物体边界)。
- 尺度不变性:DoG 在尺度空间中检测特征点,具有一定的尺度不变性,适用于多尺度的特征点检测。而 RoG 并没有直接涉及尺度空间,它更侧重于图像的局部梯度特征。
总结:
- RoG Detector:基于图像梯度的特征检测方法,用于寻找图像中的重要局部区域,如边缘和纹理。
- DoG Detector:基于两种不同标准差的高斯滤波器的差值,用于多尺度特征检测,广泛应用于角点检测和尺度不变特征提取。
DoG 更常见于计算机视觉中的特征点检测(如 SIFT)中,而 RoG 相对来说比较少见,通常用于更基础的梯度分析或结合其他方法使用。
bank of filter
susan 算子 角点检测
laplacian of gaussian 滤波
xxx算子是什么意思 xxx算子
不同算子的特点 filter 区分边界
第四章 显著性检测
主观感知相关