1 绪论

1.1 什么是大数据

定义与背景

维基百科：无法用常规软件工具处理的数据集合
《大数据时代》：采用所有数据（非抽样）进行分析
Gartner：需新处理模式的海量、高增长率、多样化信息资产
背景：
数据量迅猛增长（如2001年全年流量在2013年仅需一天）
数据可挖掘的高价值（社会需求驱动精细化管理）

特点（4V）

Volume：规模大，资源消耗高
Velocity：产生速度快，实时性要求高
Variety：来源与形式多样
Value：价值密度低但总量大

1.2 哪里有大数据

来源：
互联网（社交网络、日志、富媒体）
事业单位/政府（医疗影像、电网信息）
大型设备（波音787飞行数据、风力发电机）
工业领域

1.3 什么是大数据分析

定义与层次

定义：通过统计方法提取有用信息并形成结论的过程
三个层次：

描述分析：聚类、可视化（历史数据总结）
预测分析：回归、分类（未来趋势预测）
因果分析：回溯原因，优化决策

应用案例

宏观经济：淘宝CPI预测（基于网购数据）
制造业：库存管理与需求分析
农业：Climate公司产量预测（气候/土壤模型）
金融：德温特公司情绪分析（3.4亿留言）

1.4 大数据分析的技术与难点

分析流程

业务理解 → 2. 数据理解 → 3. 数据准备 → 4. 建模 → 5. 评估 → 6. 部署

关键技术

数据采集：MySQL/Oracle/NoSQL（应对高并发挑战）
数据管理：
NoSQL：非关系型（Key-value、文档、图数据库）
NewSQL：兼顾NoSQL扩展性与传统SQL特性
基础架构：MapReduce、Spark、HDFS
数据理解：自然语言处理（分词、实体识别）、数据清洗
统计分析：回归分析、主成分分析等
数据挖掘：分类、预测、关联规则挖掘
可视化：文本/网络/时空数据可视化

核心难点

可扩展性：支持大规模数据的高效分析
可用性：结果需高质量且符合实际需求
领域知识结合：算法需适配多样化的领域约束
结果检验：需建模验证以避免灾难性错误

2 大数据分析模型

大数据分析模型

大数据分析模型建立方法

分析模型的建立步骤

业务调研
向业务部门调研，明确数据分析任务
准备数据
根据业务需求准备相应数据
浏览数据
通过可视化等方法发现潜在关联
变量选择
基于目标选择自变量，定义因变量
定义/发现模式
建立变量间关系模型，如 y=f(x₁,x₂,…,xₙ)
计算模型参数
通过算法学习参数
模型解释与评估
专家业务解释和结果评价

应用案例：预测学生成绩

业务目标
基于学生行为数据预测成绩
关键步骤
收集起床时间、体检记录等多元数据
使用特征工程筛选高相关变量
采用多元线性回归建模
参数学习与业务解释（如血压平方对成绩影响）

基本统计量

集中趋势度量

均值
$\bar{x}=\frac{\sum x_i}{n}$
不足：易受极端值影响
中位数
有序序列中间值
不足：未充分利用所有数据
众数
最高频数值
不足：重复次数相近时无意义

统计量	优势	局限性
平均数	信息利用率高	受极端值影响
中位数	抗极端值	数据利用不足

波动性度量

极差
Max – Min
简单但信息量有限
方差/标准差
$\sigma_x^2=\frac{1}{n}\sum(x_i-\bar{x})^2$
单位不一致，计算复杂

相关性分析

皮尔森相关系数
$\rho_{X,Y}=\frac{cov(X,Y)}{\sigma_X\sigma_Y}$
范围[-1,1]，绝对值越大相关性越强
注意：相关≠因果

推断统计

参数估计方法

点估计
矩估计法
用样本矩估计总体矩
例：均匀分布参数a,b估计
极大似然估计
$\hat{\theta}=\argmax_\theta L(x_1,...,x_n;\theta)$
例：0-1分布的参数p估计
区间估计
通过置信水平/区间评估估计可靠性

核心公式示例

矩估计
均匀分布参数解：
$\hat{a}=E(X)-\sqrt{3E(X^2)-3E(X)^2}$
极大似然估计
对数似然方程：
$\frac{\partial}{\partial\theta}\ln L=0$
0-1分布解：
$\hat{p}=\frac{1}{n}\sum x_i=\overline{X}$

3 大数据关联分析模型

3.1 回归分析

基本概念与类型

定义 用于确定两种或多种变量间相互依赖的定量关系的统计分析方法，常用于预测和变量关系挖掘。
主要类型
- 一元线性回归 $y = \beta_0 + \beta_1 x + \varepsilon$ 最小二乘法目标：\underset{w}{\min}\,||Xw - y||_2^2
- 逻辑回归 $h(x) = \frac{1}{1 + e^{-(\theta^T x + b)}}$ 特点：输出范围为(0,1)，适用于二分类问题。

数学模型与检验

矩阵表示 $y = C\beta + \varepsilon$，其中 $C$ 为设计矩阵，$\beta$ 为回归系数。
模型检验
- 拟合优度检验 通过决定系数 \overline{R^2} 评估模型拟合效果： $\overline{R^2} = 1 - \frac{SSE/(n-m-1)}{SST/(n-1)}$
- 残差分析
  - 序列独立性：DW检验 r_1 = \frac{\sum_j (e_j - e_{j-1})^2}{\sum_j e_j^2}
  - 正态性检验：Q-Q图验证残差分布。

拓展模型

多元线性回归 $y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_n x_n$
多项式回归 通过引入高次项扩展线性模型，如 y = \beta_0 + \beta_1 x + \beta_2 x^2。

3.2 关联规则分析

基本概念

定义 发现数据集中项集间的频繁模式与相关性，典型应用如购物篮分析。
核心指标
- 支持度 $\text{support}(X \rightarrow Y) = \frac{\text{count}(X \cup Y)}{N}$
- 置信度 $\text{confidence}(X \rightarrow Y) = \frac{\text{count}(X \cup Y)}{\text{count}(X)}$

常用算法

Apriori算法 基于频繁项集生成与剪枝的迭代方法，核心思想：
- 频繁项集的子集必为频繁项集。
- 通过逐层搜索生成候选项集。
FP-growth算法 通过构建FP树压缩数据，避免多次扫描数据库： 1. 构建FP树与项头表 2. 挖掘条件模式基生成频繁项集

评估指标扩展

提升度 $\text{lift}(X \rightarrow Y) = \frac{\text{support}(X \cup Y)}{\text{support}(X) \cdot \text{support}(Y)}$
兴趣因子 用于衡量规则的非对称相关性，与提升度等价于二元变量。

3.3 相关分析

基本方法

定义 描述变量间关系密切程度的统计方法，如皮尔逊相关系数。
典型相关分析 研究两组变量间的整体相关性：
- 构建典型变量 U = a_1 x_1 + \cdots + a_p x_p 和 V = b_1 y_1 + \cdots + b_q y_q。
- 最大化相关系数 \rho = \frac{\text{Cov}(U, V)}{\sqrt{\text{Var}(U) \cdot \text{Var}(V)}}

应用场景

消费与收入关系分析 通过典型变量提取消费特征（如文化消费）与家庭特征（如收入、教育程度）的关联。
变量降维 通过多对典型变量逐步提取两组变量的主要相关性。

计算示例

相关系数矩阵 计算两组变量间的相关系数矩阵，筛选显著相关关系： $\text{Corr}(X, Y) = \frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum (x_i - \bar{x})^2 \sum (y_i - \bar{y})^2}}$

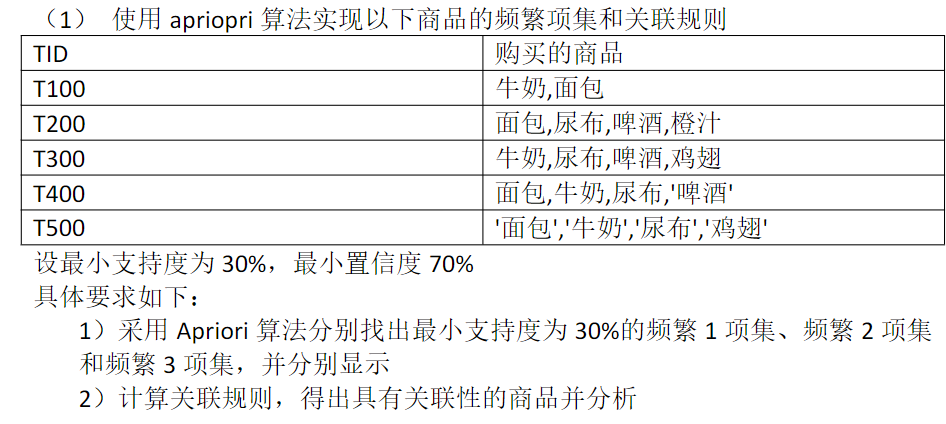
详细阐述Apriori算法和FP-growth算法

演示Apriori

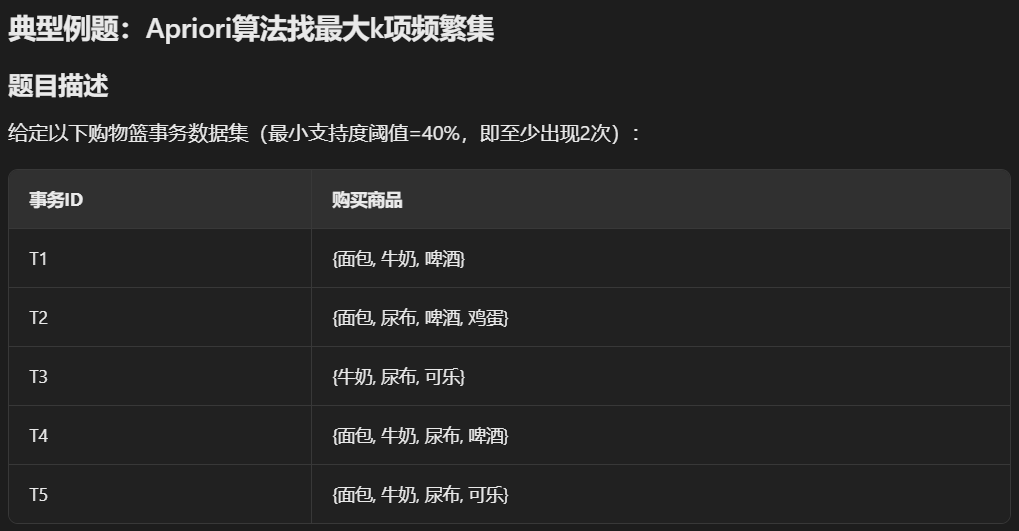
典型例题：Apriori算法找最大k项频繁集

题目描述

给定以下购物篮事务数据集（最小支持度阈值=40%，即至少出现2次）：

事务ID	购买商品
T1	{面包, 牛奶, 啤酒}
T2	{面包, 尿布, 啤酒, 鸡蛋}
T3	{牛奶, 尿布, 可乐}
T4	{面包, 牛奶, 尿布, 啤酒}
T5	{面包, 牛奶, 尿布, 可乐}

解题步骤

步骤1：生成候选1-项集（C₁）并计算支持度

项集	支持度计数	支持度
{面包}	4	4/5=80%
{牛奶}	4	80%
{啤酒}	3	60%
{尿布}	4	80%
{鸡蛋}	1	20%
{可乐}	2	40%

筛选频繁1-项集（L₁）：删除支持度<40%的项集 → 移除{鸡蛋}

步骤2：生成候选2-项集（C₂）

通过L₁自连接生成：

{面包,牛奶}, {面包,啤酒}, {面包,尿布}, {面包,可乐},
{牛奶,啤酒}, {牛奶,尿布}, {牛奶,可乐},
{啤酒,尿布}, {啤酒,可乐},
{尿布,可乐}

计算支持度：

项集	支持度计数	支持度
{面包,牛奶}	3	60%
{面包,啤酒}	3	60%
{面包,尿布}	3	60%
~~{面包,可乐}~~	1	20%
{牛奶,啤酒}	2	40%
{牛奶,尿布}	3	60%
~~{牛奶,可乐}~~	1	20%
{啤酒,尿布}	2	40%
~~{啤酒,可乐}~~	0	0%
{尿布,可乐}	2	40%

筛选频繁2-项集（L₂）：保留支持度≥40%的项集 → 移除含{可乐}的3个项集

步骤3：生成候选3-项集（C₃）

通过L₂自连接生成（需满足前k-2项相同）(此处为3-2=1)：

{面包,牛奶,啤酒}, {面包,牛奶,尿布}, {面包,啤酒,尿布}, {牛奶,啤酒,尿布}

剪枝检查（所有子集是否在L₂中）：

{面包,牛奶,啤酒}的子集：{面包,牛奶}, {面包,啤酒}, {牛奶,啤酒} → 全部在L₂
{牛奶,啤酒,尿布}的子集：{牛奶,啤酒}, {牛奶,尿布}, {啤酒,尿布} → 全部在L₂

计算支持度：

项集	支持度计数	支持度
{面包,牛奶,啤酒}	2	40%
{面包,牛奶,尿布}	2	40%
{面包,啤酒,尿布}	2	40%
~~{牛奶,啤酒,尿布}~~	1	20%

筛选频繁3-项集（L₃）：保留前3个项集

步骤4：生成候选4-项集（C₄）

通过L₃自连接生成：

{面包,牛奶,啤酒,尿布}

剪枝检查：

子集{面包,牛奶,啤酒}, {面包,牛奶,尿布}, {面包,啤酒,尿布}, {牛奶,啤酒,尿布} → 最后一个不在L₃中

终止条件：无法生成有效的4-项集

最终结果

最大频繁项集（k=3）：

{面包,牛奶,啤酒}, {面包,牛奶,尿布}, {面包,啤酒,尿布}

关键过程可视化

C₁ → L₁（频繁1-项集）
{面包}, {牛奶}, {啤酒}, {尿布}, {可乐}

C₂ → L₂（频繁2-项集）
{面包,牛奶}, {面包,啤酒}, {面包,尿布}, 
{牛奶,啤酒}, {牛奶,尿布}, {啤酒,尿布}

C₃ → L₃（频繁3-项集）
{面包,牛奶,啤酒}, {面包,牛奶,尿布}, {面包,啤酒,尿布}

C₄ → 无法生成（算法终止）

教学要点：

通过逐层生成候选集和剪枝避免组合爆炸

每次迭代需验证子集是否频繁（Apriori性质）

最大k值由数据分布和最小支持度共同决定

FP-growth

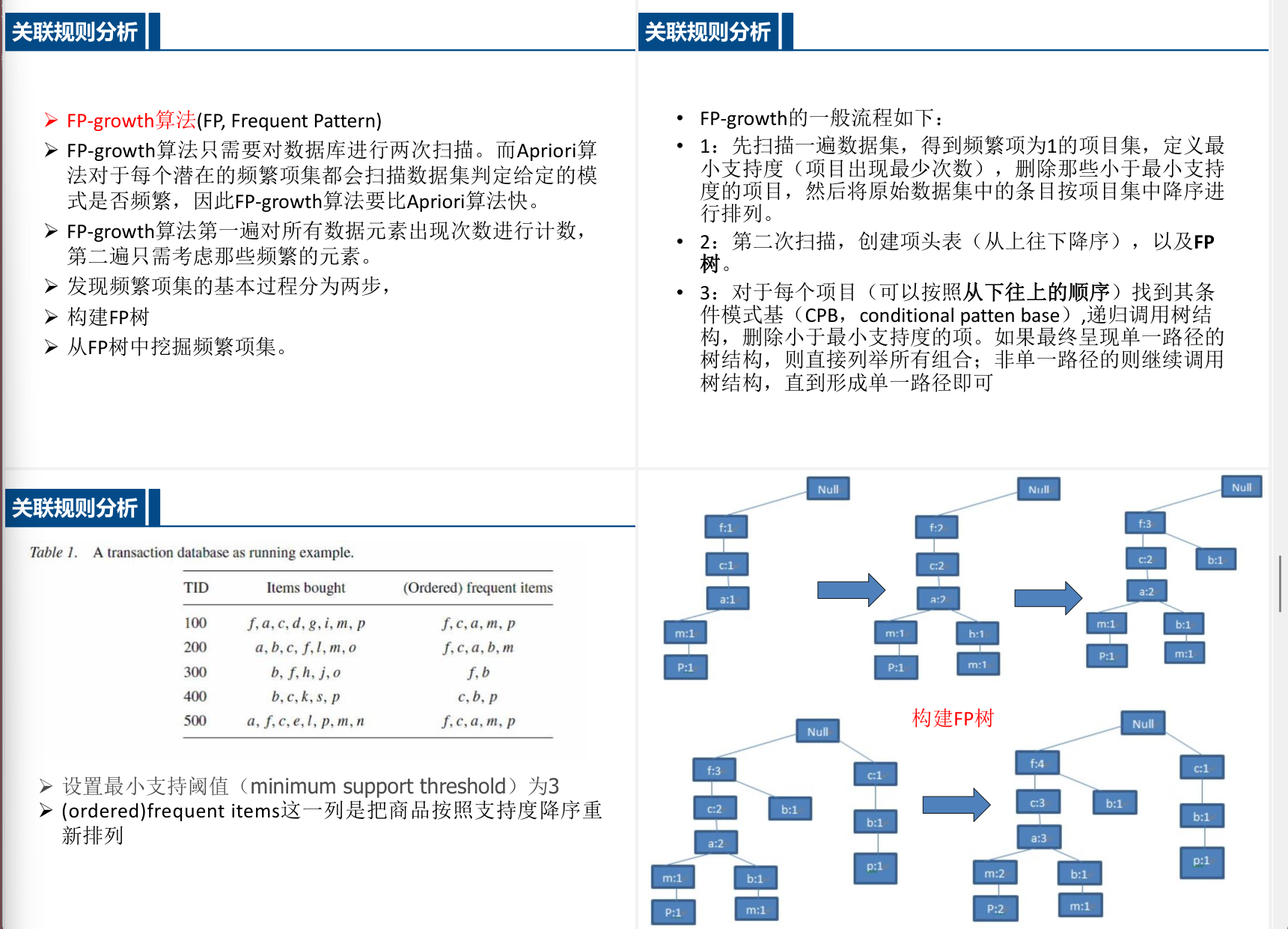
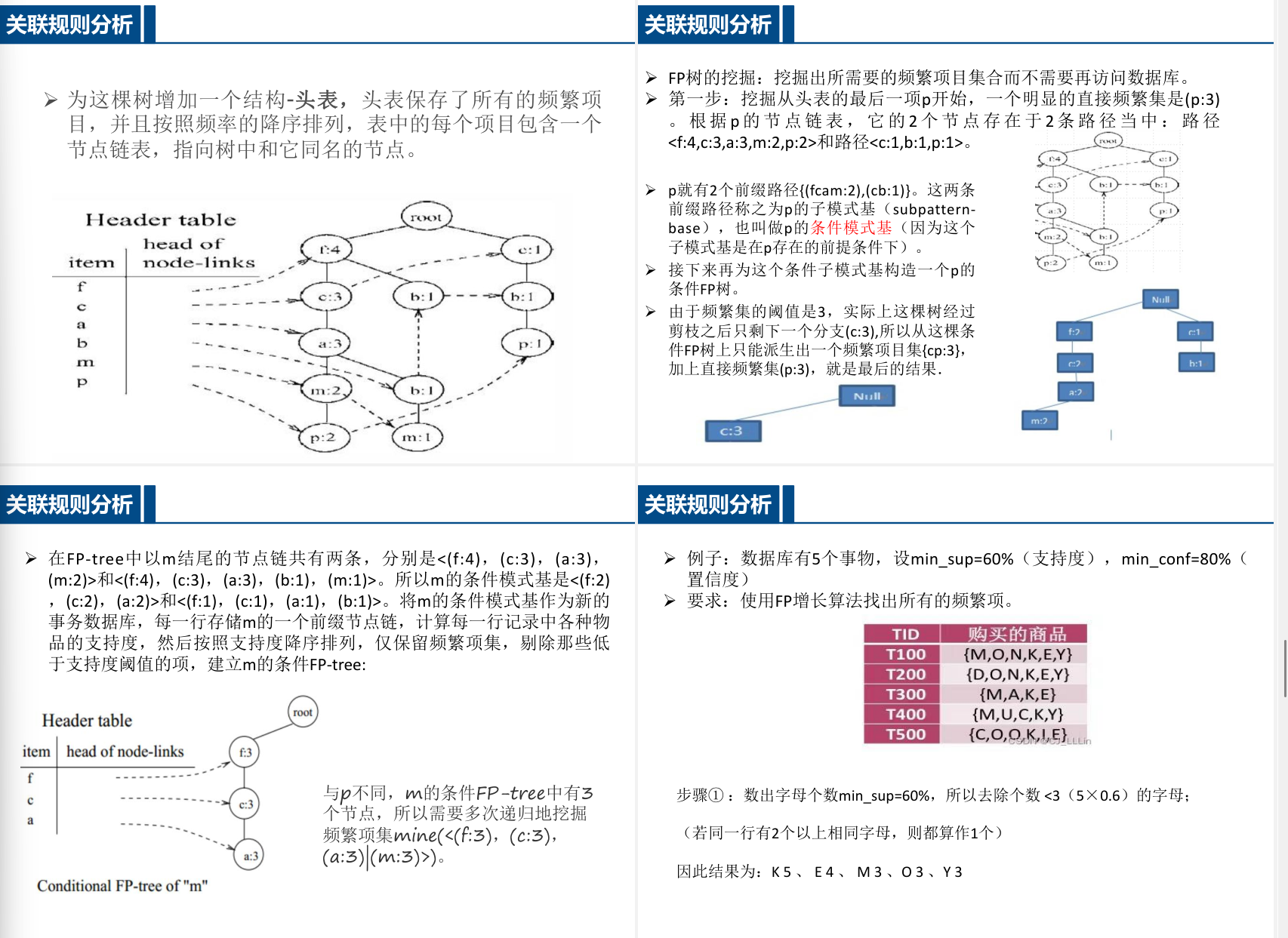
FP-growth 要画树

FP-growth算法教学案例

题目描述

给定以下购物篮事务数据集（最小支持度阈值=40%，即至少出现2次）：

事务ID	购买商品
T1	{面包, 牛奶, 啤酒}
T2	{面包, 尿布, 啤酒, 鸡蛋}
T3	{牛奶, 尿布, 可乐}
T4	{面包, 牛奶, 尿布, 啤酒}
T5	{面包, 牛奶, 尿布, 可乐}

解题步骤

步骤1：第一次扫描 – 统计项频次并排序

商品项	频次	支持度
面包	4	80%
牛奶	4	80%
尿布	4	80%
啤酒	3	60%
可乐	2	40%
鸡蛋	1	20%

筛选频繁项：删除支持度<40%的项 → 移除{鸡蛋}
排序结果（按频次降序）：面包 > 牛奶 > 尿布 > 啤酒 > 可乐

步骤2：第二次扫描 – 构建FP树

事务重排序（按频繁项顺序）：(很重要的一步,将原始数据按频繁项顺序排,删除非平凡1项集:鸡蛋)

T1: {面包,牛奶,啤酒} → {面包,牛奶,啤酒}
T2: {面包,尿布,啤酒,鸡蛋} → {面包,尿布,啤酒}
T3: {牛奶,尿布,可乐} → {牛奶,尿布,可乐}
T4: {面包,牛奶,尿布,啤酒} → {面包,牛奶,尿布,啤酒}
T5: {面包,牛奶,尿布,可乐} → {面包,牛奶,尿布,可乐}

FP树构建过程：很简单,就从上往下(只要排了序,不难)

NULL-面-牛-啤

然后面尿啤接上(从面开分支) 计数还是一样+1

FP Tree算法原理总结 – 刘建平Pinard – 博客园

4 分类分析模型

1. 分类分析基础

1.1 定义与范畴

分类分析：在已知类别下判定新对象归属 “分类分析是指在已知研究对象已经分为若干类的情况下，确定新的对象属于哪一类”
分类策略：
- 判别分析：基于统计方法（如线性判别函数）
- 机器学习模型：复杂结构判别（如决策树、SVM）

1.2 分类类型

组数划分：
- 二分类（如A/B类判别）
- 多分类（如C类判别）
方法划分：
- 参数化方法（如Fisher判别）
- 非参数化方法（如K近邻）

2. 判别分析方法

2.1 距离判别法

核心思想： \underset{i}{\arg\min}\,d(x,c_i)
距离类型：
- 马氏距离： D^2(x, G_i)=(x-\mu_i)^T\Sigma_i^{-1}(x-\mu_i)
- 相对距离：考虑类间方差的分界点计算

2.2 Fisher判别法

投影优化： “找到投影变换使类间样本分开，类内样本聚集” \Delta(\alpha)=\frac{\alpha^T B \alpha}{\alpha^T E \alpha}
判别过程：
- 计算临界值： y_0=\frac{n_1\overline{y^{(1)}}+n_2\overline{y^{(2)}}}{n_1+n_2}
- 比较投影值与临界值

2.3 贝叶斯判别法

核心改进：
- 引入先验概率： P(\pi_i|x)=\frac{p_i f_i(x)}{\sum p_j f_j(x)}
- 考虑错判损失： g^*(x)=\underset{i}{\arg\min}\sum_{j\neq i}L(j|i)P(\pi_j|x)

3. 机器学习模型

3.1 支持向量机(SVM)

优化目标： \arg\min_{w,b}\frac{1}{2}||w||^2 \quad s.t.\ y_i(w^Tx_i+b)\geq1
关键技术：
- 核函数处理线性不可分
- 松弛变量允许误分类

3.2 逻辑回归

模型结构： h_\theta(x)=\frac{1}{1+e^{-\theta^Tx}}
损失函数： J(\theta)=-\frac{1}{m}\sum [y^{(i)}\log(h_\theta(x^{(i)}))+(1-y^{(i)})\log(1-h_\theta(x^{(i)}))]

3.3 决策树与随机森林

ID3算法：
- 基于信息增益： IG(F)=H(D)-H(D|F)
随机森林： “通过行采样和列采样构建多棵决策树，投票决定最终分类”

3.4 其他模型

K近邻：基于邻居多数投票
朴素贝叶斯： P(y|x_1,...,x_n)\propto P(y)\prod_{i=1}^n P(x_i|y)

4. 模型评估

4.1 欠拟合问题

特征：
- 训练集误差高
- 模型复杂度不足
解决方案：
- 增加特征量
- 提升模型复杂度

4.2 过拟合问题

特征：
- 训练/测试误差差距大
- 模型记忆噪声数据
解决方案：
- 数据增强
- 正则化约束
# L2正则化示例 loss = cross_entropy + lambda * torch.norm(weights, p=2)

5 大数据计算平台-Spark

1. Spark概述

1.1 基本概念

Spark：基于内存计算的分布式并行计算框架，由UC Berkeley AMP实验室于2009年开发 “Spark用十分之一的计算资源，获得了比Hadoop快3倍的速度”
Scala：Spark主要编程语言，支持函数式编程和JVM兼容性 val rdd = sc.textFile("hdfs://path") // 示例RDD创建代码

1.2 与Hadoop对比

Hadoop局限：
- 磁盘IO开销大
- 仅支持MapReduce两阶段计算
Spark优势：
- 内存计算：T_{iter} = \sum_{i=1}^{n} (T_{mem\_access})
- DAG执行引擎：支持多阶段任务流水线

2. Spark生态系统

2.1 核心组件

Spark Core：提供RDD抽象和基础API rdd.filter(lambda x: "error" in x).count() # 转换+动作操作
Spark SQL：支持结构化查询，兼容Hive语法

2.2 应用场景

批处理：替代MapReduce（小时级）
流处理：微批处理（秒级延迟） “Spark Streaming无法实现毫秒级实时响应”

3. 运行架构

3.1 关键概念

RDD：弹性分布式数据集，特性包括：
- 不可变性
- 分区存储
- 血缘关系（Lineage）
DAG调度：
\text{Stage} = \text{DAG.splitByShuffleDependency()}

3.2 执行流程

窄依赖：单分区到单分区（如map）
宽依赖：Shuffle操作（如groupByKey） // 示例Java代码 JavaRDD<String> lines = sc.textFile("data.txt"); JavaRDD<Integer> lengths = lines.map(s -> s.length());

4. 部署实践

4.1 部署模式

Standalone：独立集群模式
YARN模式：资源利用率提升30%+ “统一部署可避免数据跨集群迁移”

4.2 开发流程

REPL交互：通过Spark Shell快速验证 ./bin/spark-shell --master yarn
SBT打包：构建完整应用 libraryDependencies += "org.apache.spark" %% "spark-core" % "3.0.0"

5. 性能优化

5.1 内存管理

序列化：Kryo序列化提升2-5x速度
缓存策略：MEMORY_ONLY vs DISK_ONLY

5.2 分区策略

数据倾斜：skew = \frac{max(partitions)}{avg(partitions)}
重分区：repartition(200)平衡负载

6 大数据计算平台-流计算 Spark Streaming

核心主题：大数据流计算技术

1.1 流计算基础概念

1.1.1 数据分类

静态数据：预先存储的固定数据集（如Hadoop处理的离线数据）
流数据：持续到达的动态数据流（如PM2.5监测、用户点击流） “流数据具有快速持续到达、来源多样、价值随时间衰减的特性”

1.1.2 计算模式对比

批量计算：高延迟处理静态数据（如MapReduce）
实时计算：秒级响应流数据（需特殊框架支持） # 伪代码：传统批处理 vs 流处理 batch_process = HadoopJob(input=static_data) stream_process = SparkStreaming(input=live_data)

1.2 流计算技术架构

1.2.1 处理流程

数据采集层：分布式日志系统（Kafka/Flume）
- Agent-Collector-Store三级架构
实时计算层：内存计算引擎（如Spark Streaming）
- 数学表达：throughput = \frac{data\_volume}{processing\_time}

1.2.2 系统需求

性能要求：
- 每秒处理数十万条数据
- TB/PB级数据规模支持
可靠性要求：
- 分布式容错机制
- 毫秒级故障恢复

1.3 主流框架对比

1.3.1 开源框架

Spark Streaming：
- 微批处理模型（DStream抽象）
- 与Spark SQL/MLlib生态集成
Structured Streaming： // 持续处理模式示例 val query = spark.readStream .format("kafka") .start()
- 毫秒级延迟（Spark 2.3+特性）

1.3.2 商业方案

IBM InfoSphere：企业级流处理平台
Yahoo S4：早期开源分布式流框架 “商业方案在稳定性上有优势，但开源框架更灵活易扩展”

1.4 典型应用场景

1.4.1 互联网应用

实时分析：淘宝双十一广告效果追踪
- 2-3秒延迟的TB级数据处理
用户画像：实时浏览轨迹分析

1.4.2 物联网场景

智能交通：动态路线规划
- 数学建模：route\_opt = \min\limits_{path} \sum traffic\_delay
环境监测：PM2.5实时预警系统

1 绪论

1.1 什么是大数据

定义与背景

特点（4V）

1.2 哪里有大数据

1.3 什么是大数据分析

定义与层次

应用案例

1.4 大数据分析的技术与难点

分析流程

关键技术

核心难点

2 大数据分析模型

大数据分析模型

大数据分析模型建立方法

基本统计量

推断统计

3 大数据关联分析模型

3.1 回归分析

​​基本概念与类型​​

​​数学模型与检验​​

​​拓展模型​​

3.2 关联规则分析

​​基本概念​​

​​常用算法​​

​​评估指标扩展​​

3.3 相关分析

​​基本方法​​

​​应用场景​​

​​计算示例​​

详细阐述Apriori算法和FP-growth算法

典型例题：Apriori算法找最大k项频繁集

题目描述

解题步骤

步骤1：生成候选1-项集（C₁）并计算支持度

步骤2：生成候选2-项集（C₂）

步骤3：生成候选3-项集（C₃）

步骤4：生成候选4-项集（C₄）

最终结果

关键过程可视化

FP-growth

FP-growth算法教学案例

题目描述

解题步骤

步骤1：第一次扫描 – 统计项频次并排序

步骤2：第二次扫描 – 构建FP树

4 分类分析模型

1. 分类分析基础

1.1 定义与范畴

1.2 分类类型

2. 判别分析方法

2.1 距离判别法

2.2 Fisher判别法

2.3 贝叶斯判别法

3. 机器学习模型

3.1 支持向量机(SVM)

3.2 逻辑回归

3.3 决策树与随机森林

3.4 其他模型

4. 模型评估

4.1 欠拟合问题

4.2 过拟合问题

5 大数据计算平台-Spark

1. Spark概述

1.1 基本概念

1.2 与Hadoop对比

2. Spark生态系统

2.1 核心组件

2.2 应用场景

3. 运行架构

3.1 关键概念

3.2 执行流程

4. 部署实践

4.1 部署模式

4.2 开发流程

5. 性能优化

5.1 内存管理

5.2 分区策略

6 大数据计算平台-流计算 Spark Streaming

核心主题：大数据流计算技术

基本概念与类型

数学模型与检验

拓展模型

基本概念

常用算法

评估指标扩展

基本方法

应用场景

计算示例