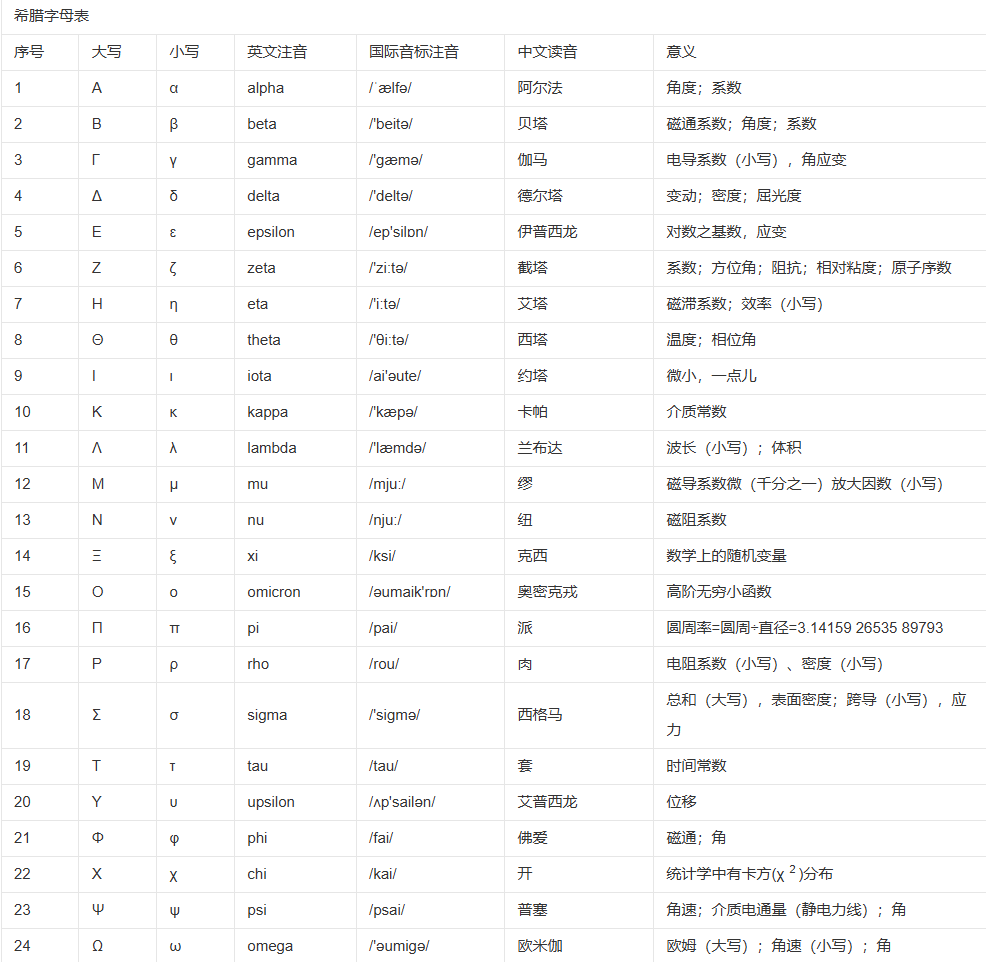
我的笔记
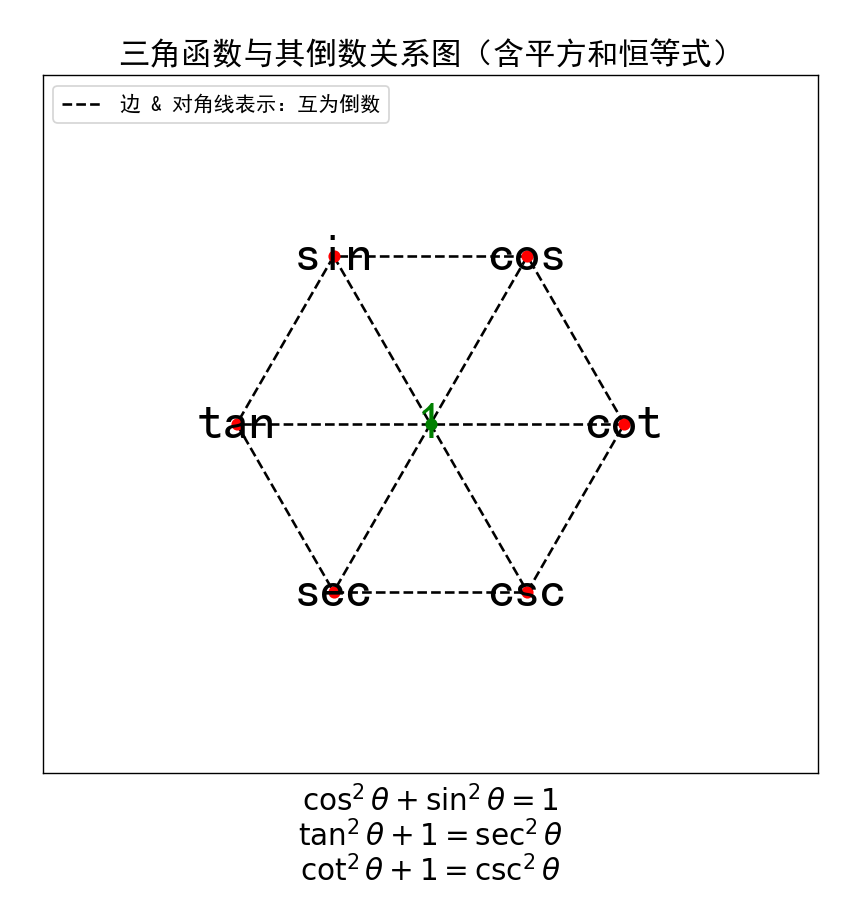
具有倒数关系的三角函数
三角恒等式:(倒三角上面两个的平方和=下面)
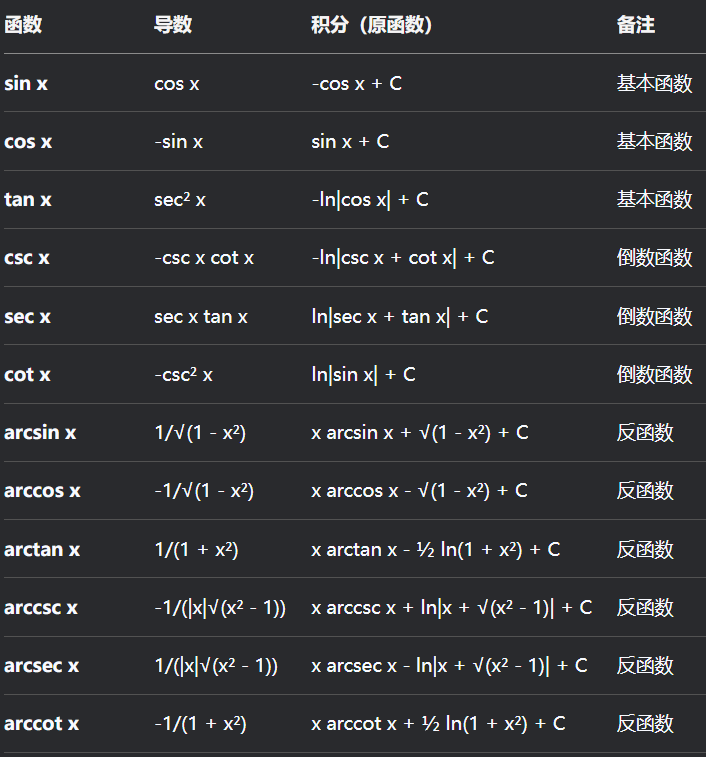
三角函数常见的求导积分

三角函数等价变换
余弦二倍角 可以利用此公式进行降幂
半角公式用余弦二倍角倒推 只有正切二倍角需要死记
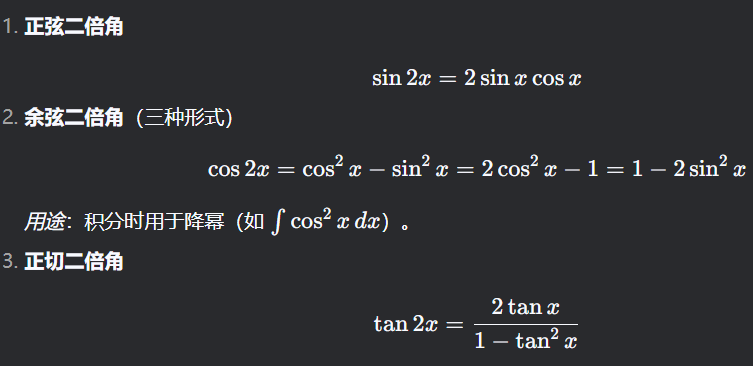
万能公式 转化三角函数名到tan
在二倍角公式的基础上 分母添加1
利用cos2x=c^2-s^2=2c^2-1=1-2s^2 除以s^2+c^2容易推导
Sin提出 Π- 不变
Cos 提出 – 不变
Tan 提出 Π 不变
利用单位圆思考 sin是单位圆上纵坐标(所以一个点先上下对称再加个180 纵坐标等于左右变换) cos是横坐标 (所以上下变换后不变 ) tan是对角不变
泰勒展开(x0=0时麦克劳林公式)







求极限 标准不定式


见到无穷比无穷或者0比0 想到洛必达和泰勒展开
常用极限e:ln(1+delta)^(1/delta) delta->0 则极限为e 其实这个本质也可以用洛必达进行证明
还是一样的取对数
见到指数就用 对数代换 然后转换为上面
注意在趋于无穷的时候 增长速率:阶乘大于指数大于幂函数大于对数 可以用夹逼准则证明]


反三角函数恒等式


计算极限时”抓大头”思想

求解定积分和不定积分可能遇到的情况以及解法
不定积分

换元法

分部积分

反对幂三指 (选择u 也就是选择保留的部分 优先级反三角函数>对数>幂函数`>三角函数>指数)
三角函数积分




定积分






是点还是坐标?
下表总结数二(高等数学一元函数部分常见)与“点”相关的核心概念,按其本质是在谈“横坐标 x”“纵坐标 y”还是“整个点 (x,y)”。(符号:x0 为某个横坐标,y0=f(x0))
| 名称(常用说法) | 定义/判定要点(数二范围简述) | 在语境中指的对象 | 备注(易混区分) |
|---|---|---|---|
| 自变量取值 | x 的具体数值 | 横坐标 | 纯数,不含函数值 |
| 函数值 | f(x0) | 纵坐标 | 又称“对应的函数值” |
| 点 / 有序对 | (x0, f(x0)) | 点 | 图像上的几何点 |
| 零点(根的横坐标) | f(x0)=0 | 横坐标 | 严格说“零点”多指 x0 |
| 函数的零点(点) | f(x0)=0 ⇒ (x0,0) | 点 | 若强调“图像上的零点” |
| x-截距 | f(x0)=0 对应 (x0,0) | 点 | 结果表现为点 |
| y-截距 | x=0 ⇒ (0, f(0)) | 点 | 有时口语上把 f(0) 叫 y 截距值(纵坐标) |
| 最大值 / 最小值(极大/极小值) | 在某区间对所有可比 f(x) 取最大/最小 | 纵坐标 | “值”= y;切勿与点混淆 |
| 最大/最小值点(极值点) | 取得最大/最小值的 (x0,f(x0)) | 点 | “极值点”=点,“极值”=纵坐标 |
| 取得极值的横坐标 | 极值所在的 x0 | 横坐标 | 又称“极值处的 x” |
| 驻点(静止点) | f'(x0)=0 且 x0 在可导区间内部 | 横坐标 | 只指 x0;对应点写 (x0,f(x0)) |
| 驻点对应的点 | 同上生成 (x0,f(x0)) | 点 | 不一定是极值点(可能拐点或平台) |
| 临界点(临界值的横坐标) | f'(x0)=0 或 f’ 不存在,且 x0 在定义域内 | 横坐标 | 含驻点 + 不可导但在域内的点 |
| 临界点对应的点 | (x0,f(x0)) | 点 | 用于极值判别的候选集合 |
| 拐点 | 凹凸性改变且曲线有切线(常用 f” 变号) | 点 | 常用判据:f” 连续且异号 |
| 凹点 / 凸点(某处凹/凸) | 描述局部曲率性质 | 点 | 单独说“凹/凸”通常指邻域性质 |
| 不可导点 | f’ 不存在 | 横坐标(或点) | 若强调位置,用 (x0,f(x0)) |
| 可导点 | f’ 存在 | 横坐标(或点) | 同上 |
| 连续点 | 极限存在且等于函数值 | 横坐标(或点) | 语境不同二选一 |
| 不连续点 | 不满足连续 | 横坐标(或点) | 分类见下几行 |
| 可去间断点 | 极限存在 ≠ 函数值或未定义,可补 | 横坐标 | 点坐标写 (x0, f(x0)或补值) |
| 跳跃间断点 | 左右极限存在且不等 | 横坐标 | y 对象是两个单侧极限(纵坐标) |
| 第二类间断点 | 至少一侧极限不存在或无穷 | 横坐标 | —— |
| 左极限 / 右极限值 | lim_{x→x0-} f(x), lim_{x→x0+} f(x) | 纵坐标 | 是数值,不是点 |
| 左/右导数值 | f’{-}(x0), f’{+}(x0) | 纵坐标 | 为导数的数值 |
| 渐近线交点(若存在) | 与坐标轴或其他渐近线交 | 点 | 例如 y=kx+b 与坐标轴交点 |
| 水平渐近线值 | y = L | 纵坐标 | L 是常数(y 值) |
| 斜/垂直渐近线位置 | x = a 或 y = kx + b | x= a → 横坐标;y=… 含 y | 视具体表达式 |
| 定积分上限 / 下限 | ∫_a^b f(x)dx 的 a,b | 横坐标 | 只是区间端点 |
| 区间端点 | 闭区间 [a,b] 的 a,b | 横坐标 | 常参与单调/极值讨论 |
| 内点 | 存在邻域全在定义域内的 x0 | 横坐标 | 拓扑概念 |
| 边界点 | 任一邻域与域内外均交 | 横坐标 | |
| 聚点(极限点) | 邻域含无限多来自集合的点 | 横坐标 | 与孤立点对比 |
| 孤立点 | 存在邻域不含其它集合点 | 横坐标 | |
| 可去奇点(扩展讨论) | 常当作可去间断点 | 横坐标 | 初级多称“可去间断” |
| 级数收敛点(x 的取值) | 幂级数收敛区间内的 x | 横坐标 | 数二对幂级数仅基础 |
| 根的重数位置 | f(x0)=0 且 (x−x0)^m | 横坐标 | m>1 为重根 |
| 单调性改变点 | 单调增/减切换的 x0 | 横坐标(或点) | 常与驻点重合 |
| 曲率改变点(=拐点) | 凹凸改变 | 点 | 同拐点 |
简要区分规则:
- 名称里带“值”通常是纵坐标(y):极大值、最小值、函数值、左极限值、导数值、极限值。
- 描述“发生在 x=?”、“满足某条件的自变量”通常是横坐标:零点(多指 x0)、驻点、临界点、间断点、端点、内点、边界点。
- 若强调“图像上的点”或含两个分量,写成 (x0, f(x0)) 才是“点”:极值点、拐点、截距点、零点的图像点、交点。
- 同一个词在不同教材可能含混:零点既可指 x0 也可指 (x0,0),答题时按题干语气(若问“求函数的零点”,给出 x;若问“在图像上零点”,可给点)。
常见易错搭配:
- 极大值 ≠ 极大值点:前者是 y,后者是 (x0, y0)。
- “求极值”题:需给极值点(x0)及相应极值 f(x0),看题目要求。
- 驻点不必是极值点:需二次导数或单侧增减性验证。
- 临界点集合 = {驻点} ∪ {不可导但在定义域内部的点}。
求导积分表
一、基本求导公式
- 幂函数:$ (x^n)’ = n x^{n-1} \ (n\in\mathbb R,\ x>0\text{ 若 }n\notin\mathbb Z)$
- 常数/常数倍:$ (C)’=0,\ (C f)’ = C f’$
- 和/差:$ (f\pm g)’ = f’ \pm g’$
- 乘积:$ (fg)’ = f’g + fg’$
- 商:$ \left(\dfrac f g\right)’ = \dfrac{f’g – fg’}{g^2}$
- 复合(链式):$ (f(g(x)))’ = f'(g(x)) g'(x)$
- 反函数:$ (f^{-1})'(y_0) = \dfrac{1}{f'(x_0)},\ y_0=f(x_0)$
- 对数:$ (\ln x)’ = \dfrac{1}{x},\ (\log_a x)’ = \dfrac{1}{x\ln a}$
- 指数:$ (e^{x})’=e^{x},\ (a^x)’ = a^x \ln a$
- 幂指混合:$ (x^{x})’ = x^{x} (1+\ln x)$($x>0$,用对数求导)
- 三角:$ (\sin x)’=\cos x,\ (\cos x)’=-\sin x,\ (\tan x)’=\sec^2 x,\ (\cot x)’=-\csc^2 x,\ (\sec x)’=\sec x\tan x,\ (\csc x)’=-\csc x\cot x$
- 反三角:$ (\arcsin x)’=\dfrac{1}{\sqrt{1-x^2}},\ (\arccos x)’=-\dfrac{1}{\sqrt{1-x^2}},\ (\arctan x)’=\dfrac{1}{1+x^2},\ (arccot x)’=-\dfrac{1}{1+x^2}$
- 双曲:$ (\sinh x)’=\cosh x,\ (\cosh x)’=\sinh x,\ (\tanh x)’=\operatorname{sech}^2 x$
- 反双曲:$ (\operatorname{arsinh} x)’=\dfrac{1}{\sqrt{1+x^2}},\ (\operatorname{artanh} x)’=\dfrac{1}{1-x^2}$
- 绝对值($x\neq0$):$ (|x|)’ = \dfrac{x}{|x|}$
二、常见复合与特殊
- $ (e^{ax})’ = a e^{ax}$
- $ (\sin(ax+b))’ = a\cos(ax+b)$
- $ (\cos(ax+b))’ = -a\sin(ax+b)$
- $ (\ln(ax+b))’ = \dfrac{a}{ax+b}$
- $ (a^{g(x)})’ = a^{g(x)} \ln a \cdot g'(x)$
- $ (e^{g(x)})’ = e^{g(x)} g'(x)$
- 对数求导:$ (f(x)^{g(x)})’ = f(x)^{g(x)} \big(g'(x)\ln f + g(x)\dfrac{f’}{f}\big)$ (先转成e的ln次方就转换成导数乘法了)
三、高阶导数常用模式
- $ (e^{ax})^{(n)} = a^{n} e^{ax}$
- $ (\sin bx)^{(n)} = b^{n} \sin\left(bx + \dfrac{n\pi}{2}\right)$
- $ (\cos bx)^{(n)} = b^{n} \cos\left(bx + \dfrac{n\pi}{2}\right)$
- $ (x^m)^{(n)} = \dfrac{m!}{(m-n)!} x^{m-n}$($m\in\mathbb N,\ n\le m$,否则为 $0$)
- 莱布尼茨:$ (fg)^{(n)} = \sum_{k=0}^{n} \binom{n}{k} f^{(k)} g^{(n-k)}$
四、隐函数 / 参数 / 极坐标
- 隐函数 $F(x,y)=0$: $ y’ = -\dfrac{F_x}{F_y}$
- 二阶:$ y” = -\dfrac{F_{xx}+2F_{xy} y’ + F_{yy}(y’)^{2}}{F_y}$
- 参数 $x=x(t), y=y(t)$:$ \dfrac{dy}{dx} = \dfrac{y’}{x’}$($x’\neq 0$),$ \dfrac{d^{2}y}{dx^{2}} = \dfrac{x’ y” – y’ x”}{(x’)^{3}}$
- 极坐标 $r=r(\theta)$:$ x=r\cos\theta,\ y=r\sin\theta,\ \dfrac{dy}{dx} = \dfrac{r’\sin\theta + r\cos\theta}{r’\cos\theta – r\sin\theta}$
五、微分与全微分
- 函数:$ dy = f'(x) dx$
- 多元:$ dz = f_x dx + f_y dy$
- 复合多元链式(单参数):$ \dfrac{dz}{dt} = f_x \dfrac{dx}{dt} + f_y \dfrac{dy}{dt}$
六、不定积分基本公式
- $ \int 0\,dx = C$
- $ \int x^{n} dx = \dfrac{x^{n+1}}{n+1} + C\ (n\neq -1)$
- $ \int \dfrac{1}{x} dx = \ln|x| + C$
- $ \int e^{ax} dx = \dfrac{1}{a} e^{ax} + C$
- $ \int a^{x} dx = \dfrac{a^{x}}{\ln a} + C$
- $ \int \sin ax\,dx = -\dfrac{1}{a} \cos ax + C$
- $ \int \cos ax\,dx = \dfrac{1}{a} \sin ax + C$
- $ \int \sec^{2} x\,dx = \tan x + C$
- $ \int \csc^{2} x\,dx = -\cot x + C$
- $ \int \sec x \tan x\,dx = \sec x + C$
- $ \int \csc x \cot x\,dx = -\csc x + C$
- $ \int \dfrac{1}{1+x^{2}} dx = \arctan x + C$
- $ \int \dfrac{1}{\sqrt{1-x^{2}}} dx = \arcsin x + C$
- $ \int \dfrac{1}{\sqrt{x^{2}+a^{2}}} dx = \ln|x+\sqrt{x^{2}+a^{2}}| + C$
- $ \int \dfrac{1}{x^{2}+a^{2}} dx = \dfrac{1}{a} \arctan \dfrac{x}{a} + C$
- $ \int \dfrac{1}{x^{2}-a^{2}} dx = \dfrac{1}{2a} \ln\left|\dfrac{x-a}{x+a}\right| + C$
- $ \int \dfrac{1}{\sqrt{a^{2}-x^{2}}} dx = \arcsin \dfrac{x}{a} + C$
- $ \int \sqrt{a^{2}-x^{2}}\,dx = \dfrac{x}{2}\sqrt{a^{2}-x^{2}} + \dfrac{a^{2}}{2}\arcsin \dfrac{x}{a} + C$
- $ \int e^{ax}\sin bx\,dx = \dfrac{e^{ax}}{a^{2}+b^{2}} (a\sin bx – b\cos bx) + C$
- $ \int e^{ax}\cos bx\,dx = \dfrac{e^{ax}}{a^{2}+b^{2}} (a\cos bx + b\sin bx) + C$
七、积分运算性质
- 线性:$ \int (af+bg) dx = a\int f dx + b\int g dx$
- 定积分可加:$ \int_{a}^{b} f = \int_{a}^{c} f + \int_{c}^{b} f$
- 反向:$ \int_{a}^{b} f = -\int_{b}^{a} f$
八、换元积分
- 一元换元:$ \int f(\varphi(t)) \varphi'(t) dt = \int f(u) du,\ u=\varphi(t)$
- 三角换元常用:
$ x=a\sin\theta \Rightarrow \sqrt{a^{2}-x^{2}}=a\cos\theta$;
$ x=a\tan\theta \Rightarrow \sqrt{x^{2}+a^{2}}=a\sec\theta$;
$ x=a\sec\theta \Rightarrow \sqrt{x^{2}-a^{2}}=a\tan\theta$
九、分部积分
- 不定:$ \int u\,dv = uv – \int v\,du$
- 定:$ \int_{a}^{b} u\,dv = [uv]{a}^{b} – \int{a}^{b} v\,du$
十、部分分式(概念)
- 若 $R(x)=\dfrac{P(x)}{Q(x)}$,$\deg P < \deg Q$ 且 $Q$ 可分解为一次/不可约二次因子,可展开为 $ \sum \dfrac{A}{(x-a)^{k}} + \sum \dfrac{Bx+C}{(x^{2}+px+q)^{m}}$,逐项积分。
十一、常见三角恒等(积分化简用)
- $ \sin^{2}x = \dfrac{1-\cos 2x}{2},\ \cos^{2}x = \dfrac{1+\cos 2x}{2}$
- $ \sin 2x = 2\sin x \cos x$
- $ \cos 2x = \cos^{2}x – \sin^{2}x = 1-2\sin^{2}x = 2\cos^{2}x -1$
- $ \sin x \sin y = \dfrac{1}{2}[\cos(x-y)-\cos(x+y)]$
- $ \cos x \cos y = \dfrac{1}{2}[\cos(x-y)+\cos(x+y)]$
- $ \sin x \cos y = \dfrac{1}{2}[\sin(x+y)+\sin(x-y)]$
十二、定积分技巧提示
- 奇偶:若 $f$ 奇,$ \int_{-a}^{a} f(x) dx = 0$;若 $f$ 偶,$ \int_{-a}^{a} f(x) dx = 2\int_{0}^{a} f(x) dx$
- 周期:$ \int_{0}^{T} f(x) dx$ 用于平均值:$ f_{\text{avg}} = \dfrac{1}{T}\int_{0}^{T} f$
- 对称换元:$ \int_{0}^{1} f(x) dx = \int_{0}^{1} f(1-x) dx$
十三、微积分联系
- 牛顿—莱布尼茨:$ \int_{a}^{b} f(x) dx = F(b)-F(a),\ F’=f$
- 导数与定积分:$ \dfrac{d}{dx} \int_{a}^{x} f(t) dt = f(x)$
- 可变上限:$ \dfrac{d}{dx} \int_{\alpha(x)}^{\beta(x)} f(t) dt = f(\beta)\beta'(x) – f(\alpha)\alpha'(x)$
十四、多元函数常用(Math II 范围内)
- 偏导定义:$ f_x(x_0,y_0)=\lim_{h\to 0} \dfrac{f(x_0+h,y_0)-f(x_0,y_0)}{h}$
- 全微分:$ df = f_x dx + f_y dy$
- 复合链式(两中间变量):若 $ z=f(u,v),\ u=u(x,y),\ v=v(x,y)$,则
$ \dfrac{\partial z}{\partial x} = f_u u_x + f_v v_x,\ \dfrac{\partial z}{\partial y} = f_u u_y + f_v v_y$ - 隐函数 $F(x,y)=0$:$ \dfrac{dy}{dx} = -\dfrac{F_x}{F_y}$
- 二元极值必要:$ f_x=0,\ f_y=0$;判别:$ D=f_{xx} f_{yy} – (f_{xy})^{2}$,$D>0,f_{xx}>0$ 极小,$D>0,f_{xx}<0$ 极大,$D<0$ 鞍点。
十五、常见易错提示
- $ \int \dfrac{f'(x)}{f(x)} dx = \ln|f(x)| + C$($f(x)\neq 0$)
- $ \int f'(x) e^{f(x)} dx = e^{f(x)} + C$
- $ \int f'(x)\sin f(x) dx = -\cos f(x) + C$,$ \int f'(x)\cos f(x) dx = \sin f(x) + C$
十六、代表性可记忆组合
- $ \int \dfrac{dx}{x\sqrt{x^{2}-a^{2}}} = \dfrac{1}{a} \operatorname{arcsec}\left|\dfrac{x}{a}\right| + C$(视教材,可换为 $ \arccos \dfrac{a}{x}$)
- $ \int \dfrac{dx}{\sqrt{ax^{2}+bx+c}}$(配方后用基本形)
简化记忆线索
- 幂指三双(幂、指数、三角、反三角、双曲、反双曲)全记导数首层。
- 积分逆向匹配导数表;含复合先看“内核导数”是否恰好出现。
- 三角平方优先半角化;乘积优先和差化;高次优先降幂。
1 极限与连续
1.1 函数
1.1.1 基本概念
函数
复合函数
反函数
基本初等函数
初等函数
1.1.2 函数的初等特性
有界性
单调性
奇偶性
周期性
1.1.3 特殊函数
符号函数
迪利克雷函数 处处不连续 处处不可导 有理数为1 无理数为0
取整函数
1.2 极限
1.2.1 基本概念
极限的定义
将epsilon理解为 精度 (挑战者,一个预期) 而根据epsilon找到的delta为应战者

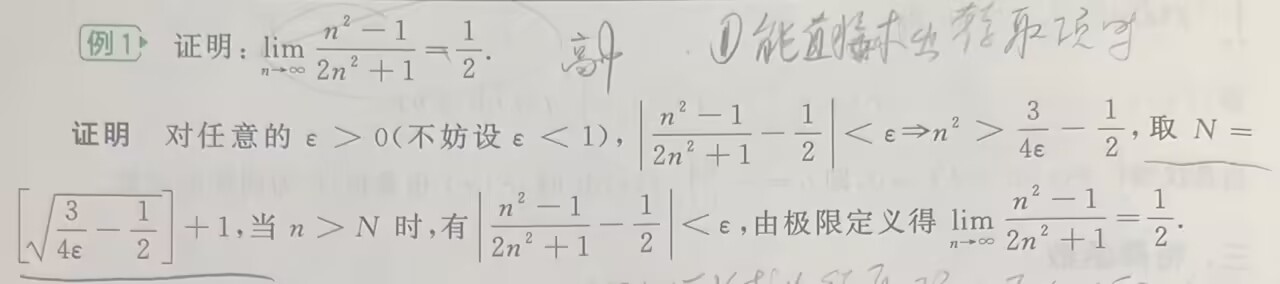



无穷小
无穷大
1.2.2 极限性质
1.2.2.1 极限的一般性质
定理一 极限的唯一性
定理二 极限的保号性
定理三 有界性
定理四 数列极限与子列极限的关系
1.2.2.2 极限的运算性质
- 四则运算性质
- 复合函数极限运算性质
1.2.2.3 极限存在准则
- 夹逼准则(迫敛定理) 数列型 函数型
- 单调有界的数列必有极限
1.2.2.4 无穷小的性质
- 无穷小的基本性质
- 等价无穷小的性质
- 当x趋近于0时,常用的等价无穷小
1.2.3 两个重要极限
lim delta->0 sin(delta)/delta =1
lim delta->0 (1+delta)^(1/delta)=e
1.3 连续与间断
1.3.1 函数连续性概念
函数fx 在点x=a处连续 <-> 设函数 fx 在x=a的领域内有定义,若函数在a处的极限等于函数值,或者说f(a+0)=f(a-0)=f(a) 那么f(x)在x=a连续
1.3.2 间断点分类
第一类间断点
包括:可去间断点(左右极限存在且相等,但是函数值不等于左右极限)
跳跃间断点(左右极限存在但不等)
第二类间断点 (左右极限至少一个不存在) 极限=无穷也叫不存在
1.4 本章重要考点以及题型
2 导数与微分
2.1 导数与微分的基本概念
fx在x=a处可导的充要条件:fx在x=a处左右导数存在(不为无穷)且相等
2.2 求导公式与法则
2.3 隐函数与参数方程确定的函数的求导
3 一元函数微分学的应用
3.1 中值定理
罗尔定理
拉格朗日中值定理
柯西中值定理
泰勒中值定理

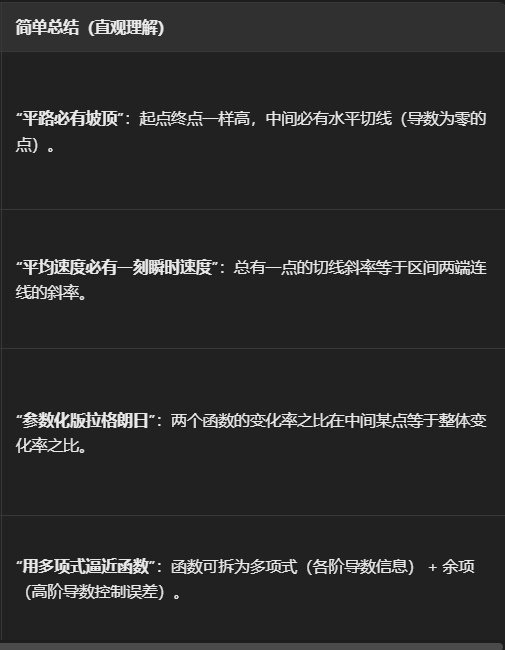
拉格朗日一般化罗尔
柯西一般化拉格朗日
3.2 单调性与极值,凹凸性与拐点,函数作图
驻点:一阶导数零点
极值点:一阶导数变号零点
鞍点:驻点而非极值点
拐点:二阶导数变号零点 一定得变号 否则跟x的三次方类似的道理
- 驻点(Stationary Points)
- •定义:一阶导数为零的点(f′(x)=0)。
- •包含关系:
- •所有极值点(可导时)和鞍点都属于驻点。
- •例如 y=x3在 x=0处是驻点,但非极值点。
- 极值点(Extrema)
- •定义:一阶导数变号的点(局部最大值或最小值)。
- •与驻点关系:
- •可导函数的极值点一定是驻点,但驻点不一定是极值点(如鞍点)。
- •不可导点可能是极值点(如 y=∣x∣在 x=0)。
- 鞍点(Saddle Points)(通常单变量函数中不出现这个)
- •定义:驻点中非极值点的点,即一阶导数为零但二阶导数不定(或 Hessian 矩阵不定)。
- •示例:z=x2−y2在 (0,0)处是鞍点。
- 拐点(Inflection Points)
- •定义:二阶导数变号的点,凹凸性改变的点。
- •与其他点的关系:
- •拐点可能是二阶导数为零或不存在的点,但需两侧变号。
- •拐点与驻点、极值点无必然包含关系(如 y=x3在 x=0既是驻点又是拐点,但非极值点)。
3.2.1单调性与极值
单调性与极值的概念
单调性判别法
若在区间I内有fx>0,则函数y=fx在区间I上严格增加;若在区间I内有fx<0,则fx在区间I严格减小
极值点的判别步骤与方法
- 确定函数的定义域
- 求fx一阶导,求出fx的驻点以及不可导点!!!
- 判别法
方法一 第一充分条件 定理 delta
方法二 第二充分条件 利用二阶导数
方法三 泰勒公式判别法
3.2.2 凹凸性与拐点
凸函数这个性质存在于函数的某一个区间
对于fx 在区间I上 如果任意f((x1+x2)/2)>(f(x1)+f(x2))/2则称fx在I上为凸函数 凸函数的整体趋势是先增后减 所以其二阶导数肯定为负 凸函数长得就像凸函数
凹函数相反
拐点的定义: 有区间I 函数fx在上面定义,若fx在x=x0两侧凹凸性不同,那么(x0,f(x0))为函数f拐点
3.2.3 渐近线
- 水平渐近线
- 铅直渐近线
- 斜渐近线
三根渐近线都与求极限有关
求水平渐近线 本质是分别求函数在正无穷和负无穷的极限
求铅直渐近线 本质是逆向思维 若lim x->a fx=∞ 说明x=a为fx的一根铅直渐近线 ,一般a选取定义域刚好不能取到的那个点
求斜渐近线 本质是在x->∞的情况下看能不能找到一个有斜率的直线, 先求limx->∞ f(x)/x=k 再用得到的k 构造lim x->∞ f(x)-kx=b
3.2.4 弧微分,曲率和曲率半径
1. 基本定义
- 弧微分(弧长微元): $ds$
- 单位切向量: $T=\dfrac{d\mathbf r/dt}{\lVert d\mathbf r/dt\rVert}$
- 曲率(无符号): $\kappa = \left\lVert \dfrac{dT}{ds} \right\rVert$
- 曲率半径: $\rho = \dfrac{1}{\kappa}$(当 $\kappa \neq 0$)
- 密切圆圆心: $\mathbf C = \mathbf r + \dfrac{1}{\kappa} \mathbf N$($\mathbf N$ 为主法向)
2. 平面显式曲线 $y=f(x)$
- 弧微分: $ds = \sqrt{1+(y’)^2},dx$
- 曲率: $\kappa = \dfrac{|y”|}{\big(1+(y’)^2\big)^{3/2}}$
- 有向曲率: $\kappa_s = \dfrac{y”}{\big(1+(y’)^2\big)^{3/2}}$
- 曲率半径: $\rho = \dfrac{\big(1+(y’)^2\big)^{3/2}}{|y”|}$
3. 平面参数方程 $\mathbf r(t)=(x(t),y(t))$
令 $x’=\dfrac{dx}{dt},\ y’=\dfrac{dy}{dt}$ 等:
- 弧微分: $ds = \sqrt{(x’)^2 + (y’)^2},dt$
- 曲率: $\kappa = \dfrac{|x’y” – y’x”|}{\big((x’)^2 + (y’)^2\big)^{3/2}}$
- 有向曲率: $\kappa_s = \dfrac{x’y” – y’x”}{\big((x’)^2 + (y’)^2\big)^{3/2}}$
- 曲率半径: $\rho = \dfrac{\big((x’)^2 + (y’)^2\big)^{3/2}}{|x’y” – y’x”|}$
4. 空间曲线 $\mathbf r(t)=(x(t),y(t),z(t))$
- 弧微分: $ds = \lVert \mathbf r'(t)\rVert dt$
- 曲率: $\kappa = \dfrac{\lVert \mathbf r'(t)\times \mathbf r”(t)\rVert}{\lVert \mathbf r'(t)\rVert^{3}}$
- 曲率半径: $\rho = \dfrac{\lVert \mathbf r'(t)\rVert^{3}}{\lVert \mathbf r'(t)\times \mathbf r”(t)\rVert}$
5. 极坐标曲线 $r = r(\theta)$
令 $r’ = \dfrac{dr}{d\theta},\ r”=\dfrac{d^2 r}{d\theta^2}$:
- 弧微分: $ds = \sqrt{r^{2} + (r’)^{2}}\ d\theta$
- 曲率: $\kappa = \dfrac{|,r^{2} + 2(r’)^{2} – r r”,|}{\big(r^{2} + (r’)^{2}\big)^{3/2}}$
- 曲率半径: $\rho = \dfrac{\big(r^{2} + (r’)^{2}\big)^{3/2}}{|,r^{2} + 2(r’)^{2} – r r”,|}$
6. 统一向量形式(平面或空间)
- 弧微分: $ds = \lVert \mathbf r'(t)\rVert dt$
- 曲率: $\kappa = \dfrac{\lVert \mathbf r'(t)\times \mathbf r”(t)\rVert}{\lVert \mathbf r'(t)\rVert^{3}}$ (平面中叉积只取标量 $x’y”-y’x”$ 的绝对值)
7. 有向曲率(平面)
- 采用参数 $t$:$\kappa_s = \dfrac{x’y” – y’x”}{\big((x’)^{2}+(y’)^{2}\big)^{3/2}}$
- 符号判定:$x’y” – y’x” > 0$ 表示朝“左”转(右手系,参数递增)
8. 物理关联
- 匀速运动速度 $v=\dfrac{ds}{dt}$,法向加速度 $a_n = v^{2}\kappa$
- 若已知加速度分解,可反求 $\kappa = \dfrac{a_n}{v^{2}}$
9. 数值计算提示
- 避免直接对噪声数据求二阶导:可用样条或局部多项式拟合
- 离散三点曲率近似:对相邻三点 $P_{i-1},P_i,P_{i+1}$, $\kappa \approx \dfrac{2\cdot \text{Area}(\triangle)}{|P_{i-1}P_i|\ |P_iP_{i+1}|\ |P_{i-1}P_{i+1}|}$
- 近直线段时 $\kappa \approx 0$,需阈值防止 $\rho=1/\kappa$ 数值发散
10. 快速对照(核心公式)
- 显式:$\kappa = \dfrac{|y”|}{(1+(y’)^{2})^{3/2}}$
- 参数 2D:$\kappa = \dfrac{|x’y”-y’x”|}{((x’)^{2}+(y’)^{2})^{3/2}}$
- 空间:$\kappa = \dfrac{\lVert \mathbf r’\times \mathbf r”\rVert}{\lVert \mathbf r’\rVert^{3}}$
- 极坐标:$\kappa = \dfrac{|r^{2}+2(r’)^{2}-r r”|}{(r^{2}+(r’)^{2})^{3/2}}$
- 曲率半径:$\rho = 1/\kappa$
3.2.5 函数作图步骤
- 求出函数定义域
- 求函数一阶导,求出驻点和不可导点
- 求fx二阶导数,求出二阶导数零点和不可导点
- 确定函数在各个小区间上fx一阶导数和二阶导数的符号,从而确定函数在各个小区间上的单调性和凹凸性
- 求出函数的水平渐近线,铅直渐近线,斜渐近线
- 找出关键点(极值点 拐点) 再描图
4 不定积分
有几个比较复杂的
1/(a^2±x^2)
1/(x^2±a^2)
1/根号下(a^2±x^2)
1/根号下(x^±a^2)
根号下(a^2±x^2)
根号下(x^2加减a^2)